Хорда, секущая, касательная

Определения

Хорда – отрезок, соединяющий две точки окружности.

В частности, хорда, проходящая через центр окружности, называется диаметром.

Секущей к окружности называется прямая, которая пересекает окружность в двух различных точках.

Касательная к окружности— прямая, имеющая с окружностью единственную общую точку.

Свойства

Радиус, проведенный в точку касания, перпендикулярен касательной

Отрезки касательных, проведенных к окружности из одной точки, равны.

Отрезки пересекающихся хорд связаны соотношением: $\color{red}AS\cdot SB=CS\cdot DS$

Произведения отрезков секущих, проведенных из одной точки, равны: $\color{red}AB\cdot AC=AD\cdot AE$

Квадрат отрезка касательной равен  произведению отрезков секущей, проведенной из той же точки: $\color{red}AB^2=AC\cdot AD$

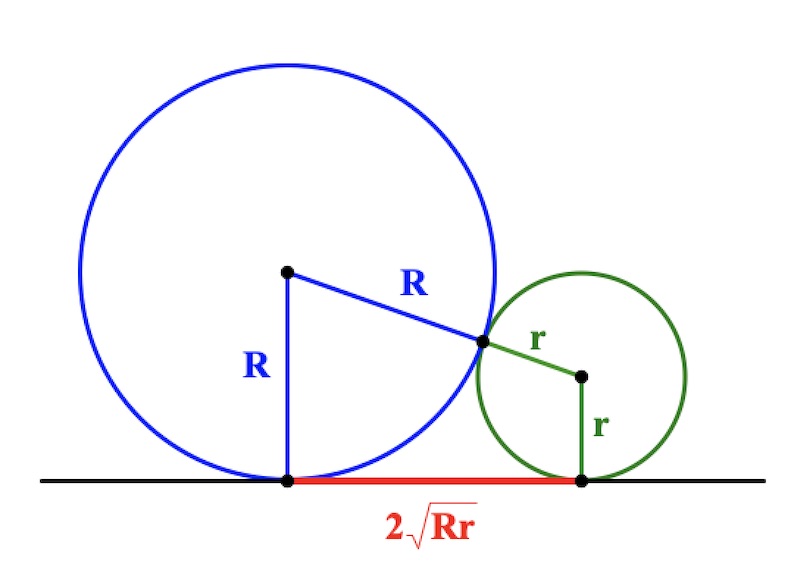
Если две окружности касаются внешним образом, то длина отрезка общей внешней касательной равна удвоенному среднему пропорциональному их радиусов  Видеодоказательство