Задача №26 ГИА Тренировочной работы А. Ларина

Елена Репина 2013-12-07 2013-12-07

Рассмотрим задачу 26 в формате ГИА по математике. Предлагалась в тренировочной работе №9 А. Лариным.

В треугольнике $ABC$ на стороне $AB$ взята точка $K$ так, что $AK:KB=1:2$ , а на стороне $BC$ взята точка $L$ так, что $CL:BL=2:1$ . Пусть $Q$ – точка пересечения прямых $AL$ и $CK$ . Найдите площадь треугольника $ABC$ , если площадь треугольника $BQC$ равна 1.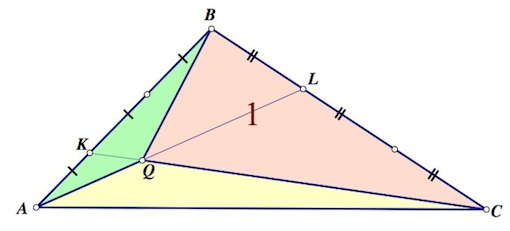

Решение:

Прежде всего заметим, что у треугольников $QBL$ и $QCL$ высоты $h$ , проведенные из вершины $Q$ совпадают. При этом $LC=2BL$ .

Поэтому площадь $\Delta QCL$ вдвое больше площади $\Delta QBL$ (Действительно, $S_{BQL}=\frac{1}{2}h\cdot BL,\;S_{CQL}=\frac{1}{2}h\cdot LC=2S_{BQL}$ ).

То есть на площадь $\Delta BQL$ приходится $\frac{1}{3}$ , на $\Delta CQL$ – $\frac{2}{3}.$

Далее замечаем, что треугольники $BQL$ и $CQL$ имеют одинаковую сторону $QL$ . Проведем высоты в каждом из названных треугольников к $QL$ .

Имеем: $2=\frac{S_{CQL}}{S_{BQL}}=\frac{\frac{1}{2}\cdot QL\cdot BT}{\frac{1}{2}\cdot QL\cdot CD}=\frac{BT}{CD}.$

То есть $CD=2BT$ . пло

Но ведь в треугольниках $ABQ$ и $CAQ$ высоты к совпавшим сторонам $AQ$ есть также $BT$ и $CD=2BT$ соответственно. Значит и $S_{ACQ}=2S_{ABQ}.$

При этом, очевидно, $S_{BKQ}=2S_{AKQ}$ (совпадают высоты, проведенные из вершины $Q$ и стороны, к которым они проведены находятся в отношении 2:1).

Пусть $S_{AKQ}=x,$ тогда $S_{BKQ}=2x$ , $S_{AQC}=6x.$

Наконец, $\frac{S_{AQC}}{S_{AKQ}}=\frac{6x}{x}=6$ и при этом $\frac{S_{AQC}}{S_{AKQ}}=\frac{\frac{1}{2}\cdot AN\cdot CQ}{\frac{1}{2}\cdot AN\cdot KQ}=\frac{CQ}{KQ}.$ Значит, $\frac{CQ}{KQ}=6$ .

Ну а значит, $\frac{S_{BQC}}{S_{BKQ}}=\frac{CQ}{KQ}=6$ (высоты, проведенные из точки $B$ к сторонам $KQ$ , $QC$ совпадают). Стало быть, $S_{BKQ}=\frac{1}{6}$ , так как $S_{BQC}=1$ . То есть $2x=\frac{1}{6}.$ Тогда площадь оставшейся части треугольника $ABC$ помимо $BQC$ , что составляет $x+2x+6x=9x$ , есть $\frac{3}{4}.$

Итак, $S_{ABC}=1+\frac{3}{4}=1,75.$

Ответ: 1, 75.

Задача для самостоятельной работы:

В треугольнике $ABC$ на стороне $AB$ взята точка $K$ так, что $AK=KB$ , а на стороне $BC$ взята точка $M$ так, что $CM:BM=1:3$ . Пусть $O$ – точка пересечения прямых $AM$ и $CK$ . Найдите отношение площадей треугольников $ABO$ и $ABC$ .

Ответ: + показать

Автор: egeMax | Нет комментариев

Печать страницы

Задача №26 ГИА Тренировочной работы А. Ларина

Добавить комментарий Отменить ответ