Задача № 26 из ГИА

Разбор геометрической  задачи из второй части тренировочной работы в формате ГИА, предлагавшейся 1 октября 2013 года.

Две окружности с центрами $O_1$и $O_3$ и радиусами 7 и 6 касаются друг с другом внешним образом и внутренним образом касаются окружности с центром $O_2$ радиусом 14. Найдите угол $O_1O_2O_3$.

Решение: 

Вот они, первые две окружности с центрами $O_1$и $O_3$. Как видим,

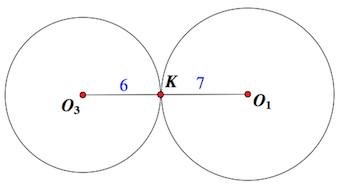
точка касания окружностей К лежит на прямой $O_1O_3$, так как согласно теореме о касающихся окружностях

Прямая, проведенная через центры касающихся окружностей, проходит через точку их касания.

Вот третья окружность, которая касается первых двух внутренним образом. Обозначим точки касания P и N. Как видим, точка $O_2$ – центр третьей окружности лежит на первой окружности.

Это не случайно.

Действительно, ведь

1) точки $O_1,\;O_2,\;N$ лежат, согласно указанной теореме, на одной прямой (так же, как и $O_2,\;O_3,\;P$)

и

2) радиус окружности с центром $O_1$ равен 7, радиус окружности с центром $O_2$ равен 14.

При этом точка $O_2$ не может попасть и на окружность с центром $O_1$, иначе диаметр окружности с центром $O_3$ ($O_2P=12$) равнялся бы радиусу окружности с центром $O_2$, то есть 14 (противоречие).

Далее, рассмотрим треугольник $O_1O_2O_3$:

В нем известны все стороны: $O_1O_2=7,\;O_2O_3=8,\;O_1O_3=13.$

Будем искать угол $O_1O_2O_3$, помеченный на рисунке как $\alpha$, по т. Косинусов:

 $O_1O_3^2=O_1O_2^2+O_2O_3^2-2O_1O_2\cdot O_2O_3\cdot cos\alpha $.

Тогда $169=64+49-2\cdot 8\cdot 7\cdot cos\alpha;$

Откуда  $cos\alpha =\frac{-56}{2\cdot 8\cdot 7};$

$cos\alpha =-\frac{1}{2};$

Следовательно, искомый угол $\alpha $ равен $120^{\circ}$.

Ответ: 120˚.