Задача 25 из тренировочной работы №1 в формате ГИА 2013

Задание 25 из второй части ТР №1 в формате ГИА от 1 октября 2013 года.

В остроугольном треугольнике ABC угол B равен 60°. Докажите, что точки A , C, центр описанной окружности треугольника ABC и точка пересечения высот треугольника ABC лежат на одной окружности.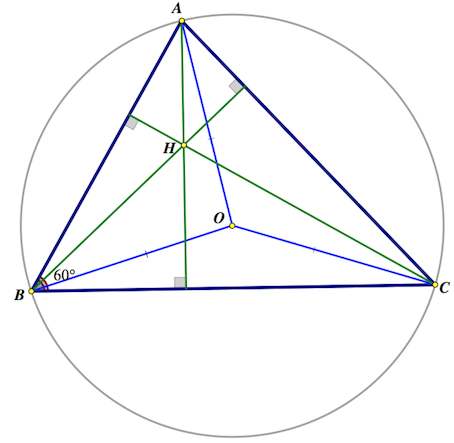

Решение:

Рассуждаем так:

Вокруг любого  треугольника, в том числе вокруг $\Delta AOC$, всегда можно описать окружность. Значит, нам остается доказать лишь тот факт, что  точка пересечения высот треугольника $ABC$, точка $H$, также попадает на окружность, описанную около треугольника $AOC$.

Заметим, что для вписанного  в окружность  (описанную около треугольника $ABC$) угла $ABC$ соответствующим центральным углом является угол $AOC$. Так как $\angle ABC=60^{\circ}$ по условию, то $\angle AOC=120^{\circ}$ по свойству вписанного угла.

Далее, из  прямоугольного треугольника $ABK$ $\angle BAK=30^{\circ}$ (так как $\angle B=60^{\circ},\;\angle K=90^{\circ}$), а значит, из прямоугольного треугольника $AHP$ $\angle AHP=60^{\circ}$.

Углы $AHP$ и $AHC$ – смежные, следовательно их сумма равна $180^{\circ}$, а значит, $\angle AHC=180^{\circ}-\angle AHP=120^{\circ}$.

В отношении точки $H$ у нас три ситуации:

(1):  точка $H$ лежит на окружности, описанной около треугольника $AOC$;

(2):  точка $H$ лежит внутри окружности, описанной около треугольника $AOC$;

(3): точка $H$ лежит вне окружности, описанной около треугольника $AOC$;

Рассмотрим ситуацию (2).

В этом случае угол $AVC$ (где $V$ – точка пересечения прямой $AH$ с окружностью), как опирающийся на ту же дугу $AC$, что и вписанный угол $AOC$, равен $120^{\circ}$. Тогда угол $AHC$, как внешний угол треугольника $HVC$, больше $120^{\circ}$ (ведь внешний угол треугольника равен сумме двух внутренних углов треугольника,  не смежных с ним). То есть мы пришли к противоречию. Ситуация (2) невозможна.

Рассмотрим ситуацию (3).

В этом случае угол $AVC$ (где $V$ – точка пересечения прямой $AH$ с окружностью), как опирающийся на ту же дугу $AC$, что и вписанный угол $AOC$, равен $120^{\circ}$. Тогда угол $AVC$, как внешний угол треугольника $HVC$, больше угла внутреннего угла треугольника $AHC$ (не смежного с внешним углом). То есть угол $AHC$ меньше $120^{\circ}$, – мы пришли к противоречию. Ситуация (3) невозможна.

Значит, остается единственно возможной ситуация (1), когда точка $H$ лежит на окружности, описанной около треугольника $AOC$. А это нам и нужно!

Итак, все четыре точки $A,\;C,\;O,\;H$  лежат на одной окружности.

Что и требовалось доказать.

Задача для самостоятельной проработки:

В остроугольном треугольнике ABC угол B равен 60° . Докажите, что точки A, C, центр описанной окружности треугольника ABC и центр вписанной

окружности треугольника ABC лежат на одной окружности.