Главная › 12 (С1) Уравнения › Задача С1 (№15) диагностической работы от 12 декабря 2013 (11 класс)

13 Дек 2013

Категория: 12 (С1) УравненияЕГЭ (диагностич. работы)Тригонометрические выражения, уравнения и неравенства

Задача С1 (№15) диагностической работы от 12 декабря 2013 (11 класс)

Елена Репина 2013-12-13 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №13»

a) Решите уравнение: $4sin^42x+3cos4x-1=0.$

б) Найдите все корни этого уравнения, принадлежащие отрезку $[\pi;\frac{3\pi}{2}].$

Решение:

а) Воспользуемся следующей формулой двойного угла для косинуса

$cos2\alpha=1-2sin^2\alpha$ .

Получим

$4sin^42x+3(1-2sin^22x)-1=0;$

$4sin^42x-6sin^22x+2=0;$

$2sin^42x-3sin^22x+1=0;$

Перед нами квадратное уравнение относительно $sin^22x:$

$2$ ( $sin^22x$ ) $^2-3$ $sin^22x$ $+1=0;$

Тогда

$sin^22x=\frac{3\pm 1}{4};$

$sin^22x=1$ или $sin^22x=\frac{1}{2};$

$sin2x=\pm 1$ или $sin2x=\pm \frac{1}{\sqrt2}$

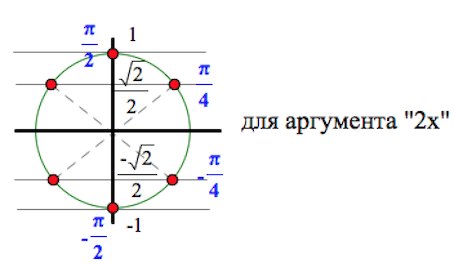
$2x=\frac{\pi}{2}+\pi n,\;n\in Z$ или $2x=\pm \frac{\pi}{4}+\pi k,\;k\in Z.$

Тогда

$x=\frac{\pi}{4}+\frac{\pi n}{2},\;n\in Z$ или $x=\pm \frac{\pi}{8}+\frac{\pi k}{2},\;k\in Z$

б) Производим отбор корней уравнения на отрезке $[\pi;\frac{3\pi}{2}]:$

Ответ: a) $\frac{\pi}{4}+\frac{\pi n}{2},\;n\in Z$ ; $\pm \frac{\pi}{8}+\frac{\pi k}{2},\;k\in Z;$ б) $\frac{9\pi}{8},\;\frac{5\pi}{4},\;\frac{11\pi}{8}.$

Смотрите также разбор заданий части В, С2(№16), C3(№17), C4(№18), С5(№20) диагностической работы по математике в формате ЕГЭ от 12 декабря 2013 года.

Возможно, вам будет интересно аналогичное задание смежного варианта:

a) Решите уравнение: $2sin^4x+3cos2x+1=0.$

б) Найдите все корни этого уравнения, принадлежащие отрезку $[\pi;3\pi].$

Ответ: + показать

Автор: egeMax | комментария 2

Печать страницы

комментария 2

Учитель

2013-12-15 в 10:36

Уважаемый коллега, по поводу С1:
уравнение вида: 2sin^4(2x) –3sin^2(2x) +2=0;
при замене переменных имеет вид:2t2 – 3t +2 = 0;
данное квадратное уравнение не имеет решения, т.к. дискриминант отрицательный… В = (-3)^2 -4*2*2 =9-16= -15
Видимо вы не совсем точно воспроизвели исходное уравнение из диагностической работы…

[ Ответить ]
- egeMax
  
  2013-12-15 в 11:42
  
  Да, спасибо большое!
  Исправила. Очепатка :)
  
  [ Ответить ]

Добавить комментарий Отменить ответ

Найти:
Материалы для подготовки к ЕГЭ
№12 №14 №15 №17
Рубрики
- 01 Геометрия (12)
- 02 Стереометрия (9)
- 03 Теория вероятностей ч.1 (1)
- 04 Теория вероятностей ч.2 (1)
- 05 Простейшие уравнения (5)
- 06 Вычисления (5)
- 07 Производная, ПО (4)
- 08 «Прикладные» задачи (5)
- 09 Текстовые задачи (7)
- 10 Графики функций (7)
- 11 Исследование функции (2)
- 12 (С1) Уравнения (79)
- 13 (С2) Стереометр. задачи (95)
- 14 (С3) Неравенства (90)
- 15 (С4) Практич. задачи (72)
- 16 (С5) Планиметр. задачи (87)
- 17 (С6) Параметры* (80)
- 18 (С7) Числа, их свойства (39)
- A1 Простейшие текст/задачи (нет в ЕГЭ-22) (3)
- A2 Читаем графики (нет в ЕГЭ-22) (1)
- Видеоуроки (44)
- ГИА (11)
  - II часть (11)
- ЕГЭ (диагностич. работы) (70)
- Задачи (34)
- Иррациональные выражения, уравнения и неравенства (15)
- Логарифмы (39)
- МГУ (12)
- Метод интервалов (4)
- Метод рационализации (18)
- Модуль (9)
- Параметр (40)
- Переменка (5)
- Планиметрия (59)
- Показательные выражения, уравнения и неравенства (8)
- Разложение на множители (1)
- Рациональные выражения, уравнения и неравенства (10)
- Справочные материалы (94)
- Стереометрия (52)
- Т/P A. Ларина (443)
- Текстовые задачи (12)
- Теория чисел (2)
- Тесты по темам (80)
- Тригонометрические выражения, уравнения и неравенства (43)
- Функции и графики (10)
Дружественные сайты
Сайт А. Ларина ЕгэТренер – О. Себедаш Математика?Легко! Егэ? Ок! – И. Фельдман
Свежие записи
Архивы Архивы