Главная › 12 (С1) Уравнения › Задание №13. Реальный ЕГЭ (Дальний Восток) от 29 мая 2019

21 Июн 2019

Категория: 12 (С1) УравненияЕГЭ (диагностич. работы)

Задание №13. Реальный ЕГЭ (Дальний Восток) от 29 мая 2019

Елена Репина 2019-06-21 2019-06-21

Условия заданий 1-19, ответы

Разбор заданий №14; №15; №16; №17; №18; №19

13. a) Решите уравнение $cos2x+\sqrt2cos(\frac{\pi}{2}+x)+1=0.$
б) Найдите его корни на промежутке $[2\pi;3,5\pi]$ .

Решение:

а)

$cos2x+\sqrt 2 cos(\frac{\pi}{2}+x)+1=0;$

$(1-2sin^2x)-\sqrt 2 sinx+1=0;$

$2sin^2x+\sqrt 2 sinx-2=0;$

$sinx=\frac{-\sqrt2 \pm 3\sqrt2}{4};$

$sinx=\frac{\sqrt2}{2};$

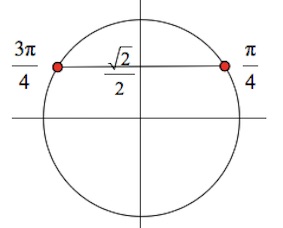
$x=\frac{\pi}{4}+2\pi n$ или $x= \frac{3\pi}{4}+2\pi n,$ $n\in Z.$

б) Корни уравнения на промежутке $[2\pi;3,5\pi]$ :

$\frac{9\pi}{4};\frac{11\pi}{4}.$

Ответ: а) $\frac{\pi}{4}+2\pi n,\frac{3\pi}{4}+2\pi n,n\in Z;$ б) $\frac{9\pi}{4};\frac{11\pi}{4}.$

Автор: egeMax | Нет комментариев

Печать страницы

Добавить комментарий Отменить ответ

Найти:
Материалы для подготовки к ЕГЭ
№12 №14 №15 №17
Рубрики
- 01 Геометрия (13)
- 02 Стереометрия (9)
- 03 Теория вероятностей ч.1 (1)
- 04 Теория вероятностей ч.2 (1)
- 05 Простейшие уравнения (5)
- 06 Вычисления (5)
- 07 Производная, ПО (4)
- 08 «Прикладные» задачи (5)
- 09 Текстовые задачи (7)
- 10 Графики функций (7)
- 11 Исследование функции (2)
- 12 (С1) Уравнения (78)
- 13 (С2) Стереометр. задачи (94)
- 14 (С3) Неравенства (89)
- 15 (С4) Практич. задачи (71)
- 16 (С5) Планиметр. задачи (86)
- 17 (С6) Параметры* (79)
- 18 (С7) Числа, их свойства (38)
- A1 Простейшие текст/задачи (нет в ЕГЭ-22) (3)
- A2 Читаем графики (нет в ЕГЭ-22) (1)
- Видеоуроки (44)
- ГИА (11)
  - II часть (11)
- ЕГЭ (диагностич. работы) (70)
- Иррациональные выражения, уравнения и неравенства (15)
- Логарифмы (39)
- МГУ (12)
- Метод интервалов (4)
- Метод рационализации (18)
- Модуль (9)
- Параметр (40)
- Переменка (5)
- Планиметрия (60)
- Показательные выражения, уравнения и неравенства (8)
- Разложение на множители (1)
- Рациональные выражения, уравнения и неравенства (10)
- Справочные материалы (92)
- Стереометрия (52)
- Т/P A. Ларина (443)
- Текстовые задачи (12)
- Теория чисел (2)
- Тесты по темам (80)
- Тригонометрические выражения, уравнения и неравенства (43)
- Функции и графики (10)
Дружественные сайты
Сайт А. Ларина ЕгэТренер – О. Себедаш Математика?Легко! Егэ? Ок! – И. Фельдман
Свежие записи
Архивы Архивы