Задание №13 Т/Р №224 А. Ларина

Смотрите также №14; №15; №16; №17; №18; №19 Тренировочной работы №224 А. Ларина.

13. Дано уравнение $4(sin4x-sin2x)=sinx(4cos^23x+3).$

а) Решите уравнение.

б) Найдите корни этого уравнения, принадлежащие отрезку $[0;\frac{3\pi}{2}]$.

Решение: 

а)

$4(sin4x-sin2x)=sinx(4cos^23x+3).$

Согласно $\color{red} sin \alpha – sin \beta = 2 sin \frac{ \alpha -\beta}{2} cos \frac{ \alpha + \beta}{2}$ имеем:

$8sinx\cdot cos3x=sinx(4cos^23x+3);$

 $sinx(4cos^23x-8cos3x+3)=0;$

$sinx=0$ или $4cos^23x-8cos3x+3=0;$

$sinx=0$ или $cos3x=\frac{4\pm2}{4};$

$sinx=0$ или $cos3x=\frac{1}{2};$

$x=\pi n$ или $3x=\pm \frac{\pi}{3}+2\pi n,$  $n\in Z;$

$x=\pi n$ или $x=\pm \frac{\pi}{9}+\frac{2\pi n}{3},$  $n\in Z.$

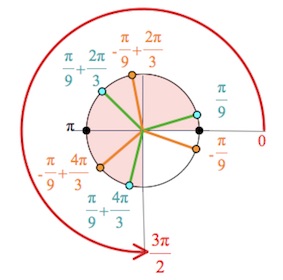
б) Корни уравнения из отрезка $[0;\frac{3\pi}{2}]$:

$0;\frac{\pi}{9};\frac{5\pi}{9};\frac{7\pi}{9};\pi; \frac{11\pi}{9};\frac{13\pi}{9}.$

Ответ: 

а) $\pi n;$  $\pm \frac{\pi}{9}+\frac{2\pi n}{3},$  $n\in Z;$

б) $0;\frac{\pi}{9};\frac{5\pi}{9};\frac{7\pi}{9};\pi; \frac{11\pi}{9};\frac{13\pi}{9}.$