Задание №14. Досрочный ЕГЭ 2018

Смотрите также задания №1-12; №13; №15; №16; №17; №18; №19

14. Дана правильная четырехугольная призма $ABCDA_1B_1C_1D_1$. На ребре
$AA_1$ отмечена точка $K$ так, что $AK:KA_1=1:2.$ Плоскость $\alpha $ проходит через точки $B$ и $K$ параллельно прямой $AC$. Эта плоскость пересекает ребро $DD_1$ в точке $M.$
а) Докажите, что $MD:MD_1=2:1.$
б) Найдите площадь сечения, если $AB=4, AA_1=6.$

Решение:

а) По свойству прямой, параллельной плоскости, плоскость $\alpha $, параллельная  $AC,$ пересечет  плоскость $AA_1C_1C,$ в которой лежит $AC,$ по некоторой прямой $l$ ($K\in l$), параллельной $AC.$

Пусть $l$ пересекается с $CC_1$ в точке $L.$ Замечаем, $CL:C_1L=1:2.$

Пусть $O,O_1$ – центры оснований призмы. Диагональные плоскости призмы пересекаются по прямой $OO_1.$

Пусть $P$ – точка пересечения $KL$ и $OO_1.$

$PB$ пересекается с $DD_1$ в точке $M.$

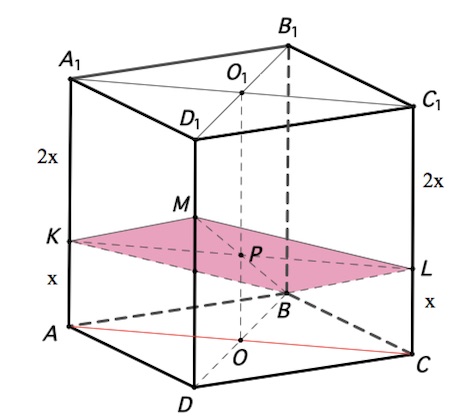
Параллелограмм $KMLB$ – сечение призмы плоскостью $\alpha .$

Пусть $AK=x,$ тогда согласно условию $A_1K=2x.$

Треугольники $BPO,BMD$ подобны, $k=BD:BO=2,$ поэтому и $DM:OP=2.$

Учитывая, что $PO=AK=x,$ получаем, что $DM=2x.$ Ну а поскольку $DD_1=3x,$ то $DM:MD_1=2x:x=2:1.$

б) Поскольку $DB\perp AC,$ то по теореме о трех перпендикулярах и $MB\perp AC.$

$AC\parallel KL,$ значит и $MB\perp KL.$

Тогда параллелограмм $KMLB$ – ромб.

$S_{KMLB}=\frac{KL\cdot MB}{2}=\frac{KL\cdot \sqrt{DM^2+DB^2}}{2}=\frac{4\sqrt2\cdot \sqrt{4^2+(4\sqrt2)^2}}{2}=8\sqrt6.$

Ответ: б) $8\sqrt6.$