Задание №14. Реальный ЕГЭ 2019 от 29 мая

Условия заданий 1-19,  ответы

Разбор заданий №13; №15; №16; №17; №18; №19

14. В правильной треугольной пирамиде $SABC$ точка $K$ делит сторону $SC$ в отношении $1:2$, считая от вершины $S$, точка $N$ делит сторону $SB$ в отношении $1:2$, считая от вершины $S$. Через точки $N$ и $K$ параллельно $SA$ проведена плоскость $\gamma$.
а) Докажите, что сечение пирамиды плоскотью $\gamma$ параллельно прямой $BC$.
б) Найдите расстояние от точки  $B$ до плоскости $\gamma$, если известно, что $SA=9,AB=6.$ 

Решение:

a) Так как $SK:KC=SN:NB,$ то (по теореме, обратной теореме Фалеса) $KN\parallel BC.$

Но тогда, так как $KN$ лежит в $\gamma,$ $BC \parallel \gamma$ по признаку параллельности прямой и плоскости.

Что и требовалось доказать.

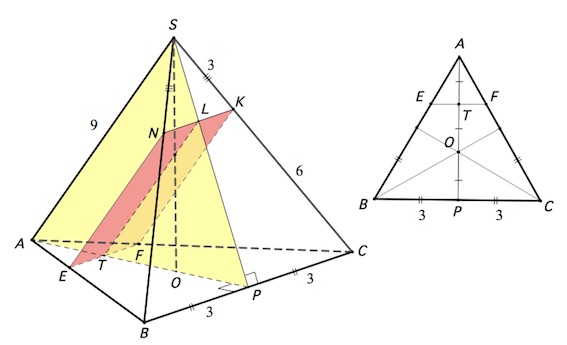
Построим сечение пирамиды плоскостью $\gamma$.

Пусть $P$– середина $BC.$ Пусть $L$ – точка пересечения $SP$ и $NK.$

Так как $AS \parallel \gamma,$ то плоскость $ASP$ пересечет $\gamma$ по некоторой прямой $l$ (проходящей через точку $L),$ параллельной $AS$ (по свойству прямой, параллельной плоскости). Пусть $l$ пересекается с $AP$ в точке $T.$ Так как  $BC \parallel \gamma,$ то $\gamma$ пересечет $ABC$ (в которой лежит $BC$) по прямой, параллельной $BC$, опять же, по свойству прямой, параллельной плоскости. Пусть точки пересечения указанной прямой со сторонами $AB,AC$ – $E$ и $F.$

Трапеция $ENKF$ – сечение пирамиды плоскостью $\gamma.$

б) Так как $BC\parallel \gamma, P\in BC$ то $\rho$($B;\gamma$)$=\rho$($P;\gamma).$

Заметим, $\gamma \perp ASP,$ так как $\gamma $ содержит прямую $EF$, перпендикулярную $ASP$ (признак перпендикулярности плоскостей). Действительно,  $EF\perp AP,$ что очевидно, а также $EF\perp TL$ по теореме о трех перпендикулярах ($AP$ – проекция $TL$ на $ABC$).

Тогда по свойству перпендикулярных плоскостей, если $PH\perp TL$ ($H\in TL$), то $PH \perp\gamma.$ Стало быть, $\rho$($P;\gamma)=PH.$

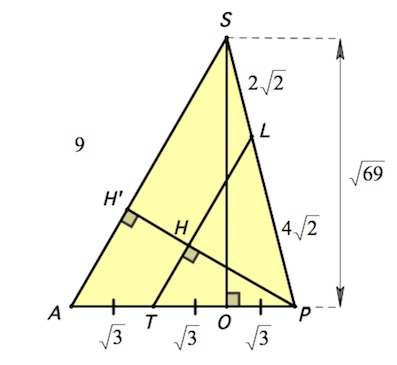
Коэффициент подобия треугольников $TLP,ASP$ – $\frac{2}{3},$ следовательно $PH=\frac{2PH_1}{3},$ где $PH_1$ – высота треугольника $ASP,$  проведенная к $AS.$

$S_{ASP}=\frac{PH_1\cdot AS}{2}=\frac{AP\cdot SO}{2};$

$PH_1=\frac{AP\cdot SO}{AS}=\frac{3\sqrt3\cdot \sqrt{69}}{9}=\sqrt{23};$

$PH=\frac{2\sqrt{23}}{3}.$

Ответ: б) $\frac{2\sqrt{23}}{3}.$