Задание №14 Т/Р №163 А. Ларина

Смотрите также №13; №15; №16; №17; №18; №19 Тренировочной работы №163 А. Ларина

14. Дана правильная шестиугольная призма $ABCDEFA_1B_1C_1D_1E_1F_1$. Через

точки $B$, $D_1$, $F_1$ проведена плоскость $\alpha $.
а) Докажите, что плоскость $\alpha $ пересекает ребро $CC_1$ в такой точке $M$, что $MC:MC_1=1:2.$
б) Найдите отношение объемов многогранников, на которые данную призму делит

плоскость $\alpha $.

Решение:

a)  Построим сечение правильной шестиугольной призмы плоскостью $\alpha =(BD_1F_1)$.

Так как параллельные плоскости пересекаются третьей по параллельным прямым, то $\alpha $ пересечет плоскость $(ABC)$ по некоторой прямой $l,$ параллельной $F_1D_1$ ($B\in l$).

Как именно построить такую прямую $l$?  Достаточно заметить, что прямая $CD$ пересекается с $l$ в некоторой точке $K$ так, что $CK:CD=1:2$ (как несложно заметить, треугольник $BCK$ – прямоугольный и в нем напротив угла в $30^{\circ}$ лежит катет, вдвое меньший гипотенузы).

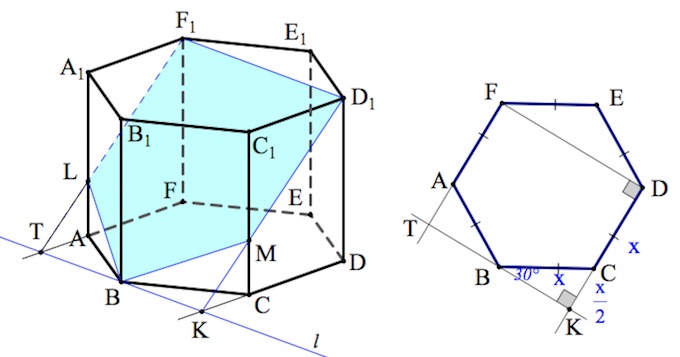
Далее, точки $D_1,K$ лежат в плоскости грани $CDD_1,$ – соединяем их прямой, которая пересекает ребро $CC_1$ в точке $M$.

Аналогичным образом $l$ пересекается с $AF$ в точке $T,$ $TF_1$ пересекается с $AA_1$ в точке $L$.

Пятиугольник $BLF_1D_1M$ – искомое сечение.

При этом,  треугольники $KMC,D_1MC_1$ подобны по двум углам и $k=KC:C_1D_1=\frac{x}{2}:x=1:2$ ($x$ – сторона основания призмы). Тогда и $MC:MC_1=1:2.$ Что и требовалось доказать.

б) Пусть $FE$ пересекается с $TK$ в точке $W,$ а $DE$ с $TK$ – в точке $P$.

Пусть прямая $PD_1$ плоскости $DEE_1$ пересекается с  прямой $EE_1$ в точке $Q$.

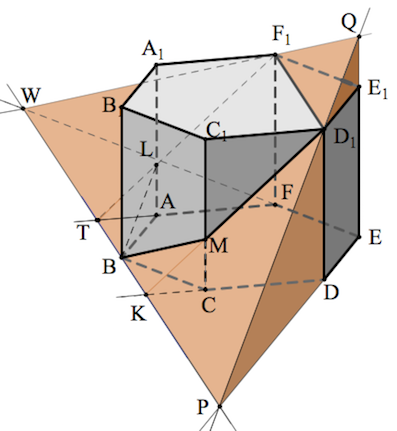
Тогда объем $V_{pod\alpha }$ части пирамиды под плоскостью $\alpha$ будем искать как  разность объема пирамиды $WPEQ$ и суммы объемов пяти пирамид $BKCM,KPDD_1,ABTL,FTWF_1,F_1D_1E_1Q.$

$V_{BKCM}=V_{ABTL}=\frac{S_{BKC}\cdot MC}{3}=\frac{\frac{BK\cdot KC}{2}\cdot \frac{H}{3}}{3},$

где $H$ – боковое ребро призмы.

$V_{BKCM}=\large\frac{\frac{\frac{\sqrt3x}{2}\cdot \frac{x}{2}}{2}\cdot H}{9}=\frac{\sqrt3x^2H}{72}.$

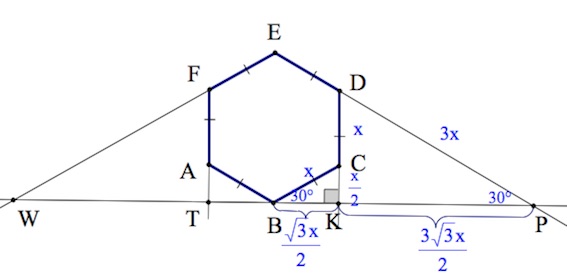
Далее

$V_{KPDD_1}=V_{FTWF_1}=\large\frac{S_{DKP}\cdot DD_1}{3}=\frac{\frac{KD\cdot KP}{2}\cdot H}{3}=\frac{\frac{\frac{3x}{2}\cdot \frac{3\sqrt3x}{2}}{2}\cdot H}{3}=\frac{3\sqrt3x^2H}{8}.$

Замечая подобие треугольников $PD_1D,D_1QE_1$ ($k=1:3$), можем утверждать, что $QE_1=\frac{H}{3}.$ Тогда

$V_{F_1D_1E_1Q}=\large\frac{S_{F_1D_1E_1}\cdot QE_1}{3}=\frac{\frac{F_1E_1^2\cdot sin120^{\circ}}{2}\cdot \frac{H}{3}}{3}=\frac{\sqrt3x^2H}{36}.$

При этом

$V_{WPEQ}=\frac{S_{WPE}\cdot QE}{3}=\large\frac{\frac{(4x)^2\cdot sin120^{\circ}}{2}\cdot \frac{4H}{3}}{3}=\frac{16\sqrt3x^2H}{9}$.

Тогда

$V_{pod\alpha }=\large\frac{16\sqrt3x^2H}{9}-(\frac{\sqrt3x^2H}{36}+\frac{3\sqrt3x^2H}{4}+\frac{\sqrt3x^2H}{36})=\frac{35\sqrt3x^2H}{36}.$

Наконец, поскольку $V_{ABCDEFA_1B_1C_1D_1E_1F_1}=\large\frac{3\sqrt 3x^2H}{2}$, объем второй части призмы $V_{nad\alpha}$ будет таков:

$V_{nad\alpha}=\large\frac{3\sqrt 3x^2H}{2}-\frac{35\sqrt3x^2H}{36}=\frac{19\sqrt3x^2H}{36}.$

Стало быть,

$V_{nad\alpha}:V_{pod\alpha }=19:35.$

Ответ: б) $19:35.$