Задание №14 Т/Р №181 А. Ларина

Смотрите также №13; №15; №16; №17; №18; №19 Тренировочной работы №181 А. Ларина 

14. В правильной пирамиде $SABC$ ребра $AB=2$, $SC=3$. Через среднюю линию $MN$ треугольника $ABC$, параллельную $AB$, проведено сечение минимальной площади пирамиды $SABC$, пересекающее ребро $SC.$
А) Докажите, что это сечение перпендикулярно ребру $SC$.

Б) Найдите площадь этого сечения.

Решение:

а) Заметим, в силу того, что пирамида $SABC$ правильная, – вершина пирамиды $S$ проецируется в центр (точку $O$)  треугольника $ABC$ (правильного).

Раз сечение проходит через точки $M,N$ и некоторую точку $T$ ребра $SC,$ в сечении – треугольник $MNT.$ Причем треугольник – равнобедеренный. Если $K$ – середина $MN,$ то $KT\perp NM.$

Площадь треугольника $MNT$ зависит от двух величин – $NM$ и $KT,$ одна из которых ($MN$) – величина постоянная. Минимальная площадь сечения – при минимальном значении $KT.$ Поскольку точка $K$ – фиксированная, то $KT$ имеет минимальную длину в случае, если $KT\perp SC.$

Заметим, $SC\perp AB,$ поскольку проекция $CH$ ($H$ – середина $AB$) прямой $SC$ на плоскость $ABC$ перпендикулярна $AB$ (применена теорема от трех перпендикулярах).

Итак, $SC\perp KT$ и $SC\perp AB,$ что говорит о том, что $SC\perp (NMT)$ по признаку перпендикулярности прямой и плоскости.

Что и требовалось доказать.

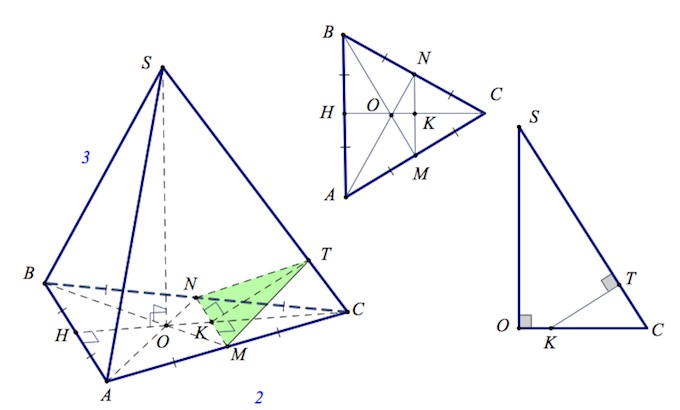
б) Заметим, так как коэффициент подобия треугольников $ABO,NMO$ – $2,$ то $OK=\frac{HO}{2}.$ Учитывая свойство медиан треугольника ($CO:OH=2:1$), получаем, что $OK=\frac{CH}{6}=\frac{OC}{4}.$

При этом $CH=\sqrt{AC^2-AH^2}=\sqrt3.$

Так как

$S_{MNT}=\frac{MN\cdot KT}{2}=\frac{1\cdot KT}{2}=\frac{KT}{2},$ то

необходимо найти $KT.$

$S_{SKC}=\frac{KT\cdot SC}{2},$ при этом $S_{SKC}=S_{SCO}-S_{SOK}=\frac{OS\cdot OC}{2}-\frac{OS\cdot OK}{2}=\frac{OS}{2}\cdot (OC-\frac{OC}{4})=$

$=\frac{OS}{2}\cdot \frac{3OC}{4}=\frac{3OS\cdot OC}{8}=\frac{3\sqrt{3^2-(\frac{2\sqrt3}{3})^2}}{8}\cdot \frac{2\sqrt3}{3}=\frac{\sqrt{23}}{4}.$

Тогда $KT=\frac{2S_{SKC}}{SC}=\frac{\frac{\sqrt{23}}{2}}{3}=\frac{\sqrt{23}}{6}.$

Наконец, $S_{MNT}=\frac{KT}{2}=\frac{\sqrt{23}}{12}.$

Ответ: $\frac{\sqrt{23}}{12}.$