Задание №14 Т/Р №196 А. Ларина

Смотрите также №13; №15; №16; №17; №18; №19 Тренировочной работы №196 А. Ларина.

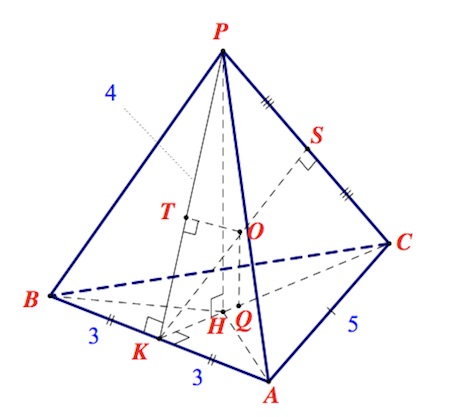
14. В основании пирамиды $PABC$ лежит равнобедренный треугольник $ABC$ $(AC=BC).$ Все боковые ребра пирамиды попарно равны. Точка $K$ – середина $AB$. В эту пирамиду вписана сфера.

а) Докажите, что точка касания сферы с гранью $APB$ лежит на прямой $PK$.

б) Найдите радиус сферы, если известно, что $AB=6,BC=5,KP=4$.

Решение:

a) Пусть $O$ – центр сферы.

Заметим, так как треугольник $APB$ равнобедренный, то  медиана $PK$ – высота  треугольника $APB.$ Аналогично $CK$ – медиана, высота и биссектриса треугольника $ABC.$

Заметим, $O$ лежит в плоскости $PCK$ – биссекторной плоскости двугранного угла, образованного плоскостями $ACP,BCP.$

Заметим также, так как все боковые ребра пирамиды равны, то вершина пирамиды проецируется  в центр описанной окружности около основания, назовем его $H.$ Очевидно, $H$ принадлежит  $CK.$

Плоскость $PCK$ при этом перпендикулярна  плоскости $ABP,$ так как в плоскости $ABP$ содержится перпендикуляр $AB$ к плоскости $PCK$  (действительно, $AB\perp CK,AB\perp PH$).

Если $T$ – точка касания сферы с гранью $ABP,$ то  $OT\perp ABP.$ Допустим, точка $T$ не принадлежит прямой $PK.$ Но по свойству перпендикулярных плоскостей можно провести из точки $O$ перпендикуляр $OT_1$ к $PK$ и он окажется перпендикуляром к плоскости $ABP.$ Но тогда треугольник $OTT_1$ содержит два прямых угла – противоречие. То есть $T$ совпадает с $T_1$ и лежит на $PK.$

Что и требовалось доказать.

б) 

Будем использовать формулу

$\color{red}V=\frac{1}{3}\cdot S\cdot r$

($V,\;S$ – объем, площадь поверхности пирамиды, $r$ – радиус вписанной сферы).

$R=AH=CH=\frac{AC\cdot BC\cdot AB}{4S}=\frac{5\cdot 5\cdot 6}{4S}=\frac {25}{8}.$

$KH=KC-CH=4-\frac{25}{8}=\frac{7}{8}.$

Из треугольника $KPH$:

 $PH=\sqrt{KP^2-KH^2}=\sqrt{16-\frac{49}{64}}=\frac{5\sqrt{39}}{8}.$

Тогда

$V_{ABCP}=\frac{12\cdot \frac{5\sqrt{39}}{8}}{3}=\frac{5\sqrt{39}}{2}.$

$S=S_{ABC}+S_{ABP}+2S_{ACP}=12+12+2\cdot \frac{25\sqrt3}{4}=24+\frac{25\sqrt3}{2}.$

Итак,

$\large r=\frac{\frac{3\cdot 5\sqrt{39}}{2}}{24+\frac{25\sqrt3}{2}}=\frac{15\sqrt{39}}{48+25\sqrt3}$.

Ответ: б) $\large \frac{15\sqrt{39}}{48+25\sqrt3}.$