Задание №15. Досрочный ЕГЭ 2018

Смотрите также задания №1-12; №13; №14; №16; №17; №18; №19

14. Решите неравенство  $\large \frac{6^x-4\cdot 3^x}{x\cdot 2^x-5\cdot 2^x-4x+20}\leq \frac{1}{x-5}.$

Видеорешение + показать

Решение:

$\large\frac{6^x-4\cdot 3^x}{x\cdot 2^x-5\cdot 2^x-4x+20}\leq \frac{1}{x-5};$

$\large\frac{3^x(2^x-4)}{2^x(x-5)-4(x-5)}\leq \frac{1}{x-5};$

$\large\frac{3^x(2^x-4)}{(x-5)(2^x-4)}\leq \frac{1}{x-5};$

$\large\frac{3^x}{x-5}\leq \frac{1}{x-5},x\neq 2;$

$\large\frac{3^x-1}{x-5}\leq 0,x\neq 2.$

Используя метод рационализации, получаем:

$\large\frac{x}{x-5}\leq 0,x\neq 2;$

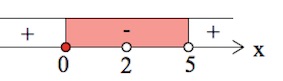
$x\in [0;2)\cup (2;5).$

Ответ: $[0;2)\cup (2;5).$