Главная › 12 (С1) Уравнения › Задание №15 Т/Р №104 А. Ларина

12 Фев 2015

Категория: 12 (С1) УравненияТ/P A. ЛаринаТригонометрические выражения, уравнения и неравенства

Задание №15 Т/Р №104 А. Ларина

Елена Репина 2015-02-12 2015-09-04

Ранее задание значилось под №15. Сейчас – под №13 (С1).

Смотрите также №16, №17, №18, №19, №20.

Дано уравнение

$\sqrt{sin2x}=\sqrt{\sqrt3cosx}.$

a) Решите уравнение;

б) Найдите его корни, принадлежащие отрезку $[4,5;7,5].$

Решение:

$\sqrt{sin2x}=\sqrt{\sqrt3cosx};$

$\begin{cases} sin2x=\sqrt3cosx,& &cosx\geq 0;& \end{cases}$

$\begin{cases} cosx(2sinx-\sqrt3)=0,& &cosx\geq 0;& \end{cases}$

$\begin{cases} \left[\begin{gathered} cosx=0,& sinx=\frac{\sqrt3}{2}; \end{gathered}\right& &cosx\geq 0;& \end{cases}$

kjj

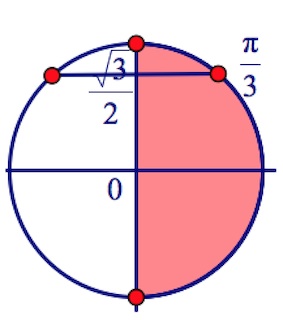
$\left[\begin{gathered} x=\frac{\pi}{2}+\pi n, n\in Z,& x=\frac{\pi}{3}+2\pi k, k\in Z; \end{gathered}\right&$

б) Отбор корней уравнения производим при помощи тригонометрического круга:

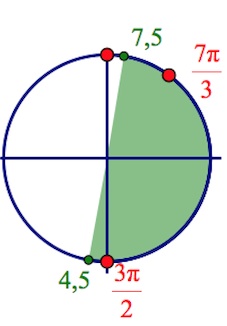
kjkjkjh

Корни уравнения из отрезка $[4,5;7,5]$ : $\frac{3\pi}{2},\frac{7\pi}{3}.$

Ответ: $\frac{3\pi}{2}, \frac{7\pi}{3}.$

Автор: egeMax | комментария 2

Печать страницы

комментария 2

Олег

2015-04-26 в 11:38

А почему вы не учитываете, что sinX>=0

[ Ответить ]
- egeMax
  
  2015-04-26 в 15:28
  
  Нет необходимости указывать, что $sin2x\geq 0$ , так как $sin2x=\sqrt3cosx$ , поэтому, указав $cosx\geq 0$ , мы учли автоматически и $sin2x\geq 0$ .
  
  [ Ответить ]

Добавить комментарий Отменить ответ

Найти:
Материалы для подготовки к ЕГЭ
№12 №14 №15 №17
Рубрики
- 01 Геометрия (12)
- 02 Стереометрия (9)
- 03 Теория вероятностей ч.1 (1)
- 04 Теория вероятностей ч.2 (1)
- 05 Простейшие уравнения (5)
- 06 Вычисления (5)
- 07 Производная, ПО (4)
- 08 «Прикладные» задачи (5)
- 09 Текстовые задачи (7)
- 10 Графики функций (7)
- 11 Исследование функции (2)
- 12 (С1) Уравнения (79)
- 13 (С2) Стереометр. задачи (95)
- 14 (С3) Неравенства (90)
- 15 (С4) Практич. задачи (72)
- 16 (С5) Планиметр. задачи (87)
- 17 (С6) Параметры* (80)
- 18 (С7) Числа, их свойства (39)
- A1 Простейшие текст/задачи (нет в ЕГЭ-22) (3)
- A2 Читаем графики (нет в ЕГЭ-22) (1)
- Видеоуроки (44)
- ГИА (11)
  - II часть (11)
- ЕГЭ (диагностич. работы) (70)
- Задачи (28)
- Иррациональные выражения, уравнения и неравенства (15)
- Логарифмы (39)
- МГУ (12)
- Метод интервалов (4)
- Метод рационализации (18)
- Модуль (9)
- Параметр (40)
- Переменка (5)
- Планиметрия (59)
- Показательные выражения, уравнения и неравенства (8)
- Разложение на множители (1)
- Рациональные выражения, уравнения и неравенства (10)
- Справочные материалы (92)
- Стереометрия (52)
- Т/P A. Ларина (443)
- Текстовые задачи (12)
- Теория чисел (2)
- Тесты по темам (80)
- Тригонометрические выражения, уравнения и неравенства (43)
- Функции и графики (10)
Дружественные сайты
Сайт А. Ларина ЕгэТренер – О. Себедаш Математика?Легко! Егэ? Ок! – И. Фельдман
Свежие записи
Архивы Архивы