Главная › 12 (С1) Уравнения › Задание №15 Т/Р №110 А. Ларина

26 Мар 2015

Категория: 12 (С1) УравненияТ/P A. ЛаринаТригонометрические выражения, уравнения и неравенства

Задание №15 Т/Р №110 А. Ларина

Елена Репина 2015-03-26 2015-09-04

Ранее задание значилось под №15. Сейчас – под №13 (С1).

Смотрите также №16, №17, №18, №19, №20.

Решите уравнение: $\sqrt{3-x^2-2x}\cdot log_2(-sin4x)=0.$

Решение:

$\sqrt{3-x^2-2x}\cdot log_2(-sin4x)=0;$

$\begin{cases} \left[\begin{gathered} 3-x^2-2x=0,& log_2(-sin4x)=0; \end{gathered}\right& &3-x^2-2x\geq 0,& &-sin4x>0;& \end{cases}$

$\begin{cases} \left[\begin{gathered} x=-3,& x=1,& -sin4x=1; \end{gathered}\right& &(x-1)(x+3)\leq 0,& &sin4x<0;& \end{cases}$

$\begin{cases} \left[\begin{gathered} x=-3,& x=1,& x=-\frac{\pi}{8}+\frac{\pi n}{2}, n\in Z; \end{gathered}\right& &-3\leq x\leq 1,& &-\frac{\pi}{4}+\frac{\pi k}{2}<x<\frac{\pi k}{2}, k\in Z;& \end{cases}$

098шгл

Ответ: $-\frac{5\pi}{8};-\frac{\pi}{8};1.$

Автор: egeMax | комментария 4

Печать страницы

комментария 4

Настя

2015-06-01 в 00:17

Объясните п-та, как число 1 вошло в ответ. С двумя другими корнями понятно

[ Ответить ]
- egeMax
  
  2015-06-01 в 07:27
  
  Настя, а какие вы видите препятствия тому, чтобы 1 вошло в ответ?
  
  [ Ответить ]
Настя

2015-06-01 в 11:03

а почему тогда -3 не берём?
не очень понятен сам промежуток одз

[ Ответить ]
- egeMax
  
  2015-06-01 в 12:09
  
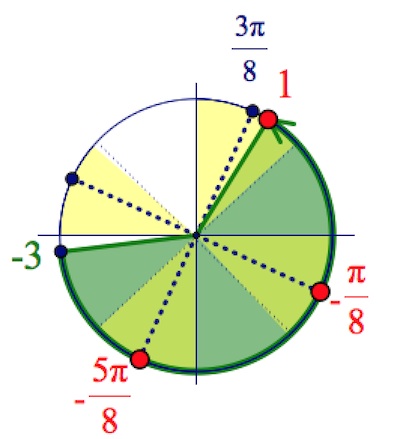
  -3 не берем, потому что -3 не удовлетворяет неравенству sin4x<0.
  На тригонометрическом круге решение указанного неравенства выделено желтым цветом.
  
  [ Ответить ]

Задание №15 Т/Р №110 А. Ларина

Добавить комментарий Отменить ответ