Главная › 12 (С1) Уравнения › Задание №13 (по старому №15) Т/Р №114 А. Ларина

23 Апр 2015

Категория: 12 (С1) УравненияТ/P A. ЛаринаТригонометрические выражения, уравнения и неравенства

Задание №13 (по старому №15) Т/Р №114 А. Ларина

Елена Репина 2015-04-23 2017-09-16

Ранее задание значилось под №15. Сейчас – под №13 (С1).

Смотрите также №16, №17, №18, №19, №20.
Дано уравнение

$cos4x-6cos2xcosx-4sin^2x+5=0$ .

а) Решите уравнение.
б) Найдите его корни, принадлежащие промежутку $[\pi;\frac{5\pi}{2}].$

Решение:

$cos4x-6cos2xcosx-4(1-cos^2x)+5=0;$

$2cos^22x-1-6cos2xcosx+4cos^2x+1=0;$

$2(2cos^2x-1)^2-6(2cos^2x-1)cosx+4cos^2x=0;$

$8cos^4x-8cos^2x+2-12cos^3x+6cosx+4cos^2x=0;$

$8cos^4x-12cos^3x-4cos^2x+6cosx+2=0;$

$4cos^4x-6cos^3x-2cos^2x+3cosx+1=0;$

7uik

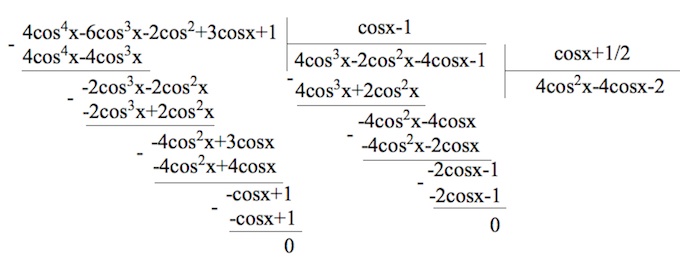
$(cosx-1)(cosx+\frac{1}{2})(4cos^2x-4cosx-2)=0;$

$(cosx-1)(cosx+\frac{1}{2})(cosx-\frac{1+\sqrt3}{2})(cosx-\frac{1-\sqrt3}{2})=0;$

$\left[\begin{gathered} cosx=1,& cosx=-\frac{1}{2},& cosx=\frac{1-\sqrt3}{2};& \end{gathered}\right&$

98ik

$x=2\pi n, n\in Z$ или $x=\pm \frac{2\pi}{3}+2\pi k, k\in Z$ или $x=\pm arccos(\frac{1-\sqrt3}{2})+2\pi t, t\in Z.$

б) Произведем отбор корней исходного уравнения из $[\pi;\frac{5\pi}{2}]$ при помощи тригонометрического круга.

Ответ:

а) $2\pi n$ , $\pm \frac{2\pi}{3}+2\pi k,$ $\pm arccos(\frac{1-\sqrt3}{2})+2\pi t, n,k,t\in Z.$

б) $\frac{4\pi}{3};2\pi-arccos(\frac{1-\sqrt3}{2});2\pi .$

Автор: egeMax | комментариев 18

Печать страницы

комментариев 18

Софья

2015-06-01 в 14:02

Здравствуйте! Подскажите, пожалуйста, как понять, что полученное выражение четвертой степени нужно делить именно на (cosx-1), а не на какое-либо другое выражение. Просто пробовать на все делить и в какой-то момент получится или все же есть определенный принцип нахождения делителя? Заранее спасибо!

[ Ответить ]
- egeMax
  
  2015-06-01 в 14:18
  
  Да, определенный принцип есть. В случае наличия целочисленных корней их следует искать среди делителей свободного члена (в данном случае свободный член 1, его делители – это 1 и -1).
  Например, при решении уравнения $x^3-x^2-8x+12=0$ целочисленные корни (а мы надеемся, что они есть) будем искать среди делителей числа 12. Вот они: $\pm 1;\pm 2;\pm 3;\pm 4;\pm 6;\pm 12.$ Берем последовательно выявленные делители свободного члена, подставляем их в исходное уравнение. Смотрим, получается ли верное равенство. Нам подойдет $2.$ Тогда $x^3-x^2-8x+12$ делим на $x-2$ . Ну и далее…
  
  [ Ответить ]
Алевтина

2016-01-16 в 00:21

Здравствуйте! А откуда взялось “2cos^2(2x)-1”?

[ Ответить ]
- egeMax
  
  2016-01-16 в 00:23
  
  Из формулы двойного угла для косинуса: $cos2\alpha=2cos^2\alpha -1.$
  
  [ Ответить ]
Maxim

2016-05-02 в 18:39

Как вы определили что делить на cosx+1/2?

[ Ответить ]
- egeMax
  
  2016-05-02 в 21:08
  
  -1/2 – корень. Поэтому, очевидно, можно нацело поделить многочлен на двучлен. Сам корень искали среди делителей свободного члена. Теорему Безу погуглите.
  Можно обойтись и без нее. Группировку сделайте.
  
  [ Ответить ]
  - Алексей
    
    2016-10-11 в 21:00
    
    Всё-таки непонятно, откуда мы должны догадаться, что -1/2 – корень. Ведь по теореме Безу делители свободного члена должны быть целочисленными, а 1/2 – дробь меньше 1.
    
    [ Ответить ]
    - egeMax
      
      2016-10-11 в 21:15
      
      Для приведенного уравнения – да. А если оно не приведенное? Как действуем, знаете?
      
      [ Ответить ]
      - Алексей
        
        2016-10-11 в 21:21
        
        Ну, наверное, делим левую и правую части уравнения на 1-й коэффициент (у наибольшей степени переменной), т.е. “приводим”…
        
        [ Ответить ]
      - egeMax
        
        2016-10-11 в 21:24
        
        … и удобно сделать некую замену с целью ухода от дробных коэффициентов. Какую? Далее работаем с приведенным уравнение…
        Несложно увидеть связь корней приведенного и первоначального…
        
        [ Ответить ]
      - Алексей
        
        2016-10-11 в 21:49
        
        Всё-таки не пойму, к чему Вы клоните. Ну разделим на 4, всё равно же будут дробные коэффициенты, а свободный член станет 1/4. Какую замену сделать? Поясните подробнее, пожалуйста.
        
        [ Ответить ]
      - egeMax
        
        2016-10-11 в 21:54
        
        Можно домножить обе части уравнения на 4^3 и сделать замену t=4x. Уравнение с t – приведенное. Его и решаем. Несложно затем выйти на x.
        
        [ Ответить ]
      - Алексей
        
        2016-10-11 в 22:24
        
        Большое спасибо!
        Теперь до меня дошло: -2 – делитель свободного члена приведённого уравнения, равного 16, корень приведённого уравнения равен t=-2, а x=t/4=-2/4= -1/2.
        Благодарю за пояснение!
        
        [ Ответить ]
      - egeMax
        
        2016-10-11 в 23:24
        
        [ Ответить ]
Ася

2017-09-15 в 21:55

Здравствуйте, возник такой вопрос по решению этого уравнения:
Если совершить преобразования, то можно свести его к виду 2*(cos2x)^2-6*cos2x*cosx+4*(cosx)^2=0
Если делением на (cosx)^2, свести к квадратному, то так решение будет проще, по -моему.
Поэтому два вопроса: можно ли так решать такое уравнение?
И является ли такое уравнение также однородным тригонометрическим уравнением или в однородных тригонометрических всегда должны быть синус и косинус в качестве разных переменных?

[ Ответить ]
- egeMax
  
  2017-09-16 в 00:32
  
  Здравствуйте! Но не видя самого уравнения, как я вам подскажу? Вижу только то, к чему свели…
  Или вы об уравнении, что разобрано выше?
  
  [ Ответить ]
  - Ася
    
    2017-09-16 в 19:23
    
    Да, именно об этом уравнении, которое рассмотрено на этой странице
    
    [ Ответить ]
    - egeMax
      
      2017-09-16 в 23:03
      
      Не вижу как вам поможет деление на cos^2x…
      
      [ Ответить ]

Задание №13 (по старому №15) Т/Р №114 А. Ларина

Добавить комментарий Отменить ответ