Задание №15 Т/Р №162 А. Ларина

Смотрите также №13; №14; №16; №17; №18; №19 Тренировочной работы №162 А. Ларина

15. Решите неравенство: $\large\frac{2^{cosx}-1}{3\cdot 2^{cosx}-1}\leq 2^{1+cosx}-2.$

Решение:

 $\large\frac{2^{cosx}-1}{3\cdot 2^{cosx}-1}\leq 2^{1+cosx}-2;$

 $\large\frac{2^{cosx}-1-(2^{1+cosx}-2)(3\cdot 2^{cosx}-1)}{3\cdot 2^{cosx}-1}\leq 0;$

 $\large\frac{2^{cosx}-1-2(2^{cosx}-1)(3\cdot 2^{cosx}-1)}{3\cdot 2^{cosx}-1}\leq 0;$

$\large\frac{2^{cosx}-1-2(3\cdot 2^{2cosx}-4\cdot 2^{cosx}+1)}{3\cdot 2^{cosx}-1}\leq 0;$

$\large\frac{-6\cdot 2^{2cosx}+9\cdot 2^{cosx}-3}{3\cdot 2^{cosx}-1}\leq 0;$

$\large\frac{2\cdot 2^{2cosx}-3\cdot 2^{cosx}+1}{2^{cosx}-\frac{1}{3}}\geq 0;$

$\large\frac{2(2^{cosx}-1)(2^{cosx}-\frac{1}{2})}{2^{cosx}-\frac{1}{3}}\geq 0;$

$\large\frac{(2^{cosx}-2^0)(2^{cosx}-2^{-1})}{2^{cosx}-2^{log_2\frac{1}{3}}}\geq 0.$

Применяем метод замены множителей:

$\frac{(cosx-0)(cosx+1)}{cosx-log_2\frac{1}{3}}\geq 0$  (*)

Так как

$log_2\frac{1}{3}<log_2\frac{1}{2}=-1$, то есть $-log_2\frac{1}{3}>1$

и

$cosx\geq -1,$

то

$cosx-log_2\frac{1}{3}>0$ при любом значении $x$.

Поэтому (*) равносильно следующему неравенству:

$cosx(cosx+1)\geq 0$ (**)

Если $cosx=-1$, то получаем верное неравенство (**). Если $cosx\neq -1,$ то $cosx+1>0$ и, сократив обе части неравенства (**) на положительную величину $cosx+1$, приходим к тому, что $cosx\geq 0.$

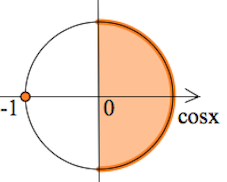
Итак, имеем

$cosx=-1$ или $cosx\geq 0;$

$x\in [-\frac{\pi}{2}+2\pi n;\frac{\pi}{2}+2\pi n]\cup${$\pi+2\pi n$}, $n\in Z.$

Ответ: $[-\frac{\pi}{2}+2\pi n;\frac{\pi}{2}+2\pi n]\cup${$\pi+2\pi n$}, $n\in Z.$