Главная › Справочные материалы › Задание №16. Досрочный ЕГЭ 2018

08 Май 2018

Категория: Справочные материалы

Задание №16. Досрочный ЕГЭ 2018

Елена Репина 2018-05-08 2018-05-08

Смотрите также задания №1-12; №13; №14; №15; №17; №18; №19

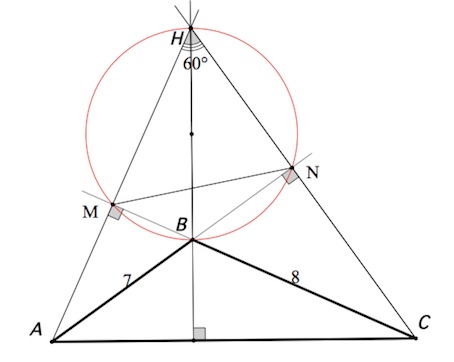
16. В треугольнике $ABC$ угол $ABC$ тупой, $H$ — точка пересечения продолжений высот, угол $AHC$ равен $60$ °.
а) Докажите, что угол $ABC$ равен $120$ °.
б) Найдите $BH$ , если $AB= 7, BC = 8.$

Решение:

a) Пусть $BC$ пересекается с $AH$ в точке $M,$ $AB$ с $CH$ – в точке $N.$

Четырехугольник $MHNB$ таков, что $\angle M+\angle N=180^{\circ}.$ Тогда и $\angle H+\angle MBN=180^{\circ}.$ То есть $\angle MBN=180^{\circ}-60^{\circ}=120^{\circ}.$ Углы $ABC, MBN$ – вертикальные, поэтому и $\angle ABC=120^{\circ}.$

б) Углы $MBA,ABC$ и $NBC,ABC$ – смежные, поэтому, раз $\angle ABC=120^{\circ},$ то $\angle MBA=\angle NBC=60^{\circ}.$

В прямоугольных треугольниках $AMB,CNB$ углы $A$ и $C$ – по $30^{\circ}.$

Тогда $MB=\frac{AB}{2}=\frac{7}{2},$ $BN=\frac{BC}{2}=4.$

По теореме косинусов из треугольника $MBN:$

$MN^2=\frac{49}{4}+16-2\cdot \frac{7}{2}\cdot 4\cdot cos120^{\circ};$

$MN^2=\frac{169}{4};$

$MN=\frac{13}{2}.$

Поскольку сумма противоположных углов четырехугольника $MHNB$ равна $180^{\circ},$ то около него можно описать окружность. Треугольник $MNH$ вписан в эту окружность. По теореме синусов $\frac{MN}{sin H}=2R,$ где $R$ – радиус окружности.

Итак,

$BH=2R=\frac{13}{2}}:{\frac{\sqrt3}{2}}=\frac{13}{\sqrt3}.$

Ответ: б) $\frac{13}{\sqrt3}.$

Автор: egeMax | комментария 2

Печать страницы

комментария 2

Пукер

2020-06-16 в 03:12

а из чего следует что BH проходит через центр окружности?

[ Ответить ]
- egeMax
  
  2020-06-16 в 16:36
  
  ВН – диаметр окружности. Все вершины прямоугольных треугольников с общей гипотенузой лежат на одной окружности, диаметр которой – гипотенуза
  
  [ Ответить ]

Задание №16. Досрочный ЕГЭ 2018

Добавить комментарий Отменить ответ