В новом формате ЕГЭ по математике задание значится как «Задание №14»
Смотрите также №15, №17, №18, №19, №20, №21.
Разбор задания №16 одного из вариантов
В основании четырехугольной пирамиды $SABCD$ лежит прямоугольник $ABCD$ со сторонами $AB=\sqrt5$ и $BC=2$.
Длины боковых ребер пирамиды $SA=\sqrt7,SB=2\sqrt3,SD=\sqrt{11}.$
а) Докажите, что $SA$ – высота пирамиды.
б) Найдите угол между прямой $SC$ и плоскостью $ASB.$
Решение:
а) Замечаем, что по теореме, обратной теореме Пифагора, треугольники $ABS,ADS$ – прямоугольные.
Действительно,
$(\sqrt7)^2+(\sqrt5)^2=(2\sqrt3)^2$
и
$(\sqrt7)^2+2^2=(\sqrt{11})^2.$
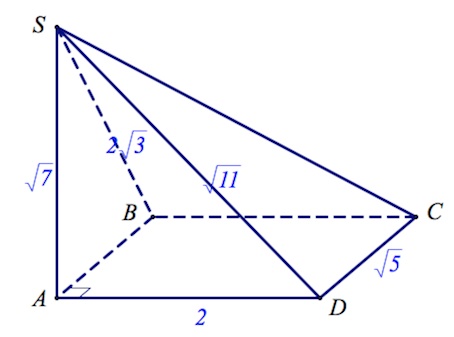
Итак, $SA\perp AD$ и $SA\perp AB.$ По признаку перпендикулярности прямой и плоскости имеем: $SA\perp ABCD$, то есть $SA$ – высота пирамиды.
Что и требовалось доказать.
б) Заметим, что $BC\perp ASB$ (во-первых, $BC\perp AB$ так как $ABCD$ – прямоугольник, во-вторых, наклонная $SB$ перпендикулярна $BC$, так как ее проекция на плоскость $ABCD$ перпендикулярна $BC$ (т. о трех перпендикулярах)).
Поэтому $\angle (SC;ABS)=\angle CSB.$

Из прямоугольного треугольника $SBC:$
$tg CSB=\frac{BC}{SB}=\frac{2}{2\sqrt3}=\frac{\sqrt3}{3},$ откуда $\angle CSB=30^{\circ}.$
Ответ: $30^{\circ}.$


Спасибо огромное,Елена Юрьевна!За такой быстрый ответ на мою просьбу:)-всё так доступно и конкретно объяснено!
а я(:-решала пункт а)-всё искала “сложности”-никак не могла поверить,что задание из 2-ой части решаются в три строчки…
Искренне благодарю,что помогли мне разобраться с этой задачей!!
а пункт б)в этой задаче я решала координатно-векторным методом-ответ получился.как у Вас-только я получила синус-а уже потом,угол=30.а Ваше решение-быстро,точно по школе,и лаконичное!-возьму себе на заметку-что порой,по школьной базе геометрии 10-11,достаточно коротко и красиво можно решать и задачу №16.
С ИСКРЕННЕЙ БЛАГОДАРНОСТЬЮ,Елена:)
Здравствуйте! За последние годы вот эта задача подарок судьбы. Спасибо!
Да уж, точно! ;)
Елена Юрьевна решите пожалуйста задачу:
ОСНОВАНИЕМ ПРЯМОЙ ТРЕУГОЛЬНОЙ ПРИЗМЫ АВСА1В1С1 ЯВЛЯЕТСЯ РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК АВС, В КОТОРОМ АВ=ВС=10, АС=16. БОКОВОЕ РЕБРО ПРИЗМЫ РАВНО 24. ТОЧКА Р-СЕРЕДИНА РЕБРА ВВ1. НАЙДИТЕ ТАНГЕНС УГЛА МЕЖДУ ПЛОСКОСТЯМИ А1В1С1 И АСР.
У МЕНЯ ПОЛУЧИЛОСЬ ТАНГЕНС РАВЕН 2. ОТВЕТ НЕ СХОДИТСЯ.
И у меня получилось 2.
А ТАМ ОТВЕТ 4/3
Может, боковое ребро 16? а не 24?
Помогите доказать :
ДАН КУБ ABCDA1B1C1D1. а) ДОКАЖИТЕ, ЧТО ПРЯМАЯ BD1 ПЕРПЕНДИКУЛЯРНА ПЛОСКОСТИ ACB1.
Найдите в плоскости ACB_1 две пересекающиеся прямые, каждая из которых перпендикулярна BD_1.
Начните… Хотя бы одну укажите…
Не понятно, а что это за квадраты складываются? Т. е. после слова “действительно, “. Поясните поподробнее . Спасибо большое!
Теорему Пифагора знаете?
Конечно! Ее же все знают! Даже русские!! Квадрат гипотенузы равен сумме квадратов катетов или наоборот. Или по-школьному: пифагоровы штаны во все стороны равны. Но там не понятно что с чем складывается, все смешано-перемешано!! В кучу.(
Там квадрат гипотенузы первого треугольника (ABS) сложили с квадратом катета второго треугольника (ADS). Где же тут теорема Пифагора?=)
На заметку: Гипотенуза – это сторона треугольника, лежащая против прямого угла. А угол S совсем не прямой во втором треугольнике (ADS).
Вы действительно думаете, что я не в состоянии отличить гипотенузу от катета?
В треугольнике ABS угол A – прямой (как выяснилось)…
И во втором треугольнике угол A также прямой.
Так что подумайте, где там катеты, а где гипотенузы…
Так во втором треугольнике гипотенуза – SD (в треугольнике ADS)?!! И тео Пифагора применима только для одного треугольника же?! Ничего не пойму.
Да, SD – гипотенуза треугольника ADS.
Вначале решения проверяется «прямоугольность» двух треугольников – ADS и ABS.
AD – это катет же?? У воторого треугольника. Какое отношение он имеет к первому треугольнику? Это же смешно!!
Катет, конечно.
К первому треугольнику не имеет ни малейшего отношения.
В чем проблема-то, Kirill?
Над чем смеемся-то?
А почему же тогда складывается гипотенуза первого треугольника с катетом второго? Где же тут теорема Пифагора? 2 в квадрате – это же катет в квадрате у второго треугольника.
Kirill, ну не складывается гипотенуза с катетом!..
[latexpage]$\Delta ABS:$
$AB^2+AS^2=SB^2,$ так как $(\sqrt5)^2+(\sqrt7)^2=(2\sqrt3)^2.$
$\Delta ADS:$
$AD^2+AS^2=SD^2,$ так как $2^2+(\sqrt7)^2=(\sqrt{11})^2.$