Главная › 13 (С2) Стереометр. задачи › Задание №16 (С2) Т/Р №92 А. Ларина

20 Ноя 2014

Категория: 13 (С2) Стереометр. задачиСтереометрияТ/P A. Ларина

Задание №16 (С2) Т/Р №92 А. Ларина

Елена Репина 2014-11-20 2016-06-11

В новом формате ЕГЭ по математике задание значится как «Задание №14»

Смотрите также №15, №17, №18, №19, №20.
Ребро куба $ABCDA_1B_1 C_1 D_1$ равно 4. Через середины ребер $AB$ и $BC$ параллельно прямой $BD_1$ проведена плоскость.
а) Постройте сечение куба этой плоскостью.
б) Найдите площадь полученного сечения.

Решение:

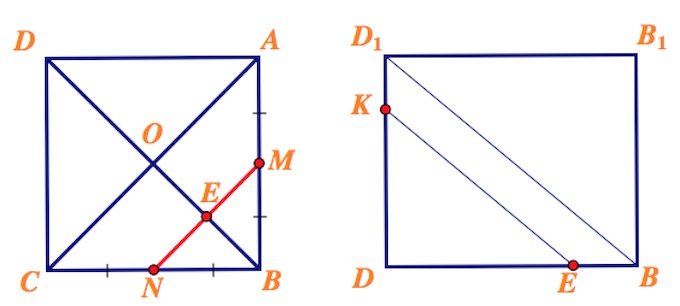
a) Построим сечение куба плоскостью, проходящей через середины $M$ и $N$ ребер $AB$ и $BC$ соответственно, паралельно прямой $BD_1.$

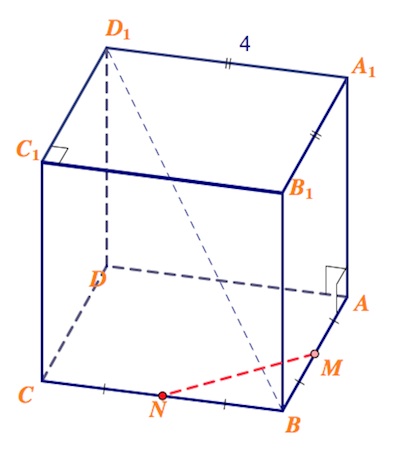длт Плоскость сечения, что мы строим, пересекает плоскость $BDD_1B_1$ , в которой лежит прямая $BD_1$ по прямой, параллельной $BD_1$ . Пусть $MN$ пересекается c $BD$ в точке $E$ . Проводим прямую $EK$ в плоскости $BDD_1B_1$ , параллельную $BD_1$ ( $K\in DD_1$ 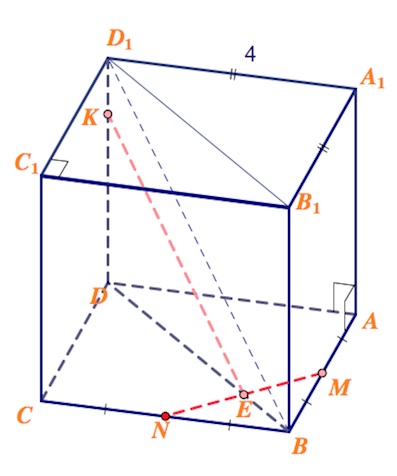). Прямая $MN$ пересекает плоскости граней $CC_1D_1D$ , $AA_1A_1D$ в точках $R$ и $S$ на прямых $CD$ и $AD$ соответственно (см. рисунок). Соединяем точки $R$ и $K$ , $S$ и $K$ . $Z$ – точка пересечения $RK$ и $CC_1$ , $H$ – точка пересечения $KS$ и $AA_1.$ 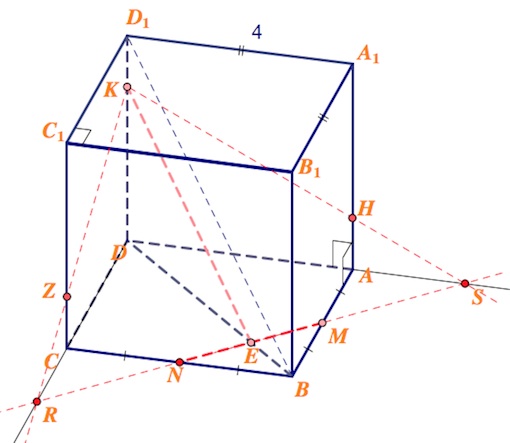lkn Пятиугольник $ZKHMN$ – искомое сечение.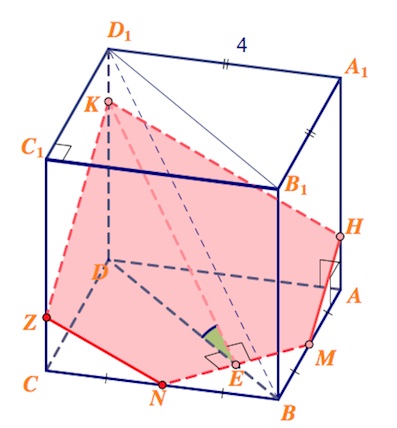

б) Площадь сечения будем искать, пользуясь формулой

$S_{sechenie}=\frac{S_{proeksia}}{cos\alpha}$ ,

где $\alpha$ – угол между плоскостями сечения и основания.

В нашем случае

$S_{sechenie}=\frac{S_{AMNCD}}{Cos\angle KED}$

$\angle KED$ – линейный угол двугранного угла, образованного плоскостями сечения и основания. Действительно, во-первых, $MN$ – средняя линия треугольника $ABC$ , а значит $MN||AC$ , при этом $AC\perp BD$ , откуда следует, что и $BD\perp MN$ . Во-вторых, по теореме о трех перпендикулярах, наклонная $KE$ перпендикулярна $MN$ , коль ее проекция $BD$ на плоскость $ABC$ , в которойлежит $MN$ , перпендикулярна $MN$ .

Найдем косинус угла $KED$ из треугольника $DEK$ :

Очевидно, $BE:BD=1:4$ , то есть $DE=\frac{3BD}{4}=\frac{3\cdot 4\sqrt2}{4}=3\sqrt2.$

l,m

Далее, $KE:BD_1=3:4$ (в силу подобия треугольников $DEK$ и $DBD_1$ с коэффициентом подобия $3:4$ , ведь мы говорили, – $BE=\frac{BD}{4}$ ), то есть $KE=\frac{3BD_1}{4}=\frac{3\cdot 4\sqrt3}{4}=3\sqrt3.$