Главная › 13 (С2) Стереометр. задачи › Задание №16 (С2) Т/Р №97 А. Ларина

25 Дек 2014

Категория: 13 (С2) Стереометр. задачиСтереометрияТ/P A. Ларина

Задание №16 (С2) Т/Р №97 А. Ларина

Елена Репина 2014-12-25 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №14»

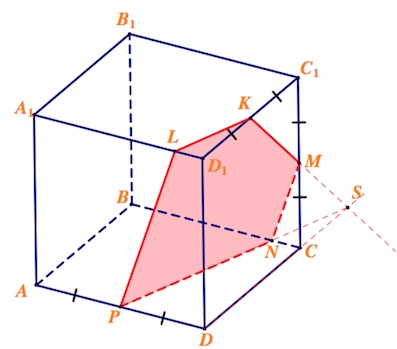
В кубе $ABCDA_1B_1C_1D_1$ точка $K$ – середина ребра $C_1D_1$ , точка $P$ – середина ребра $AD$ , точка $M$ – середина ребра $CC_1$ .

а) Постройте сечение куба плоскостью, проходящей через точки $K$ , $P$ и $M$ .
б) Найдите площадь полученного сечения, если ребро куба равно 6.

Решение:

a) Пусть прямая $KM$ пересекается с прямой $DC$ (обе лежат в плоскости грани $DCC_1$ ) в точке $S$ .

Пусть $SP$ пересекается с $BC$ в точке $N$ .

Через точку $P$ в плоскости грани $AA_1D_1$ проводим прямую, параллельную $MN$ (ведь параллельные плоскости $(BCC_1), (ADD_1)$ пересекаются плоскостью сечения по параллельным прямым (по свойству параллельных плоскостей)). Пусть указанная прямая пересекает ребро $A_1D_1$ в точке $L$ .

Сечение $LKMNP$ – искомое.

б) Проекция сечения $LKMNP$ на плоскость $ABC$ – есть пятиугольник $PNCXH$ .

Будем искать площадь сечения следующим образом (подробно – здесь):

$S_{LKMNP}=\frac{S_{PNCXH}}{cos\alpha},$

где $\alpha$ – угол между плоскостями $LKMNP$ и $PNCXH$ .

При этом $\alpha=\angle LFH$ , где $LF\perp PN$ (а значит и $FH\perp PN$ (по теореме о трех перпендикулярах)).

ijk

Далее – кратко.

Из прямоугольного треугольника $PSD:$

$PS=\sqrt{DS^2+DP^2}=\sqrt{9^2+3^2}=3\sqrt{10}.$

Пусть $RD\perp PS.$

Распишем площадь треугольника $PSD$ двумя способами:

$\frac{1}{2}\cdot RD\cdot PS=\frac{1}{2}\cdot PD\cdot DS;$

$RD=\frac{3\cdot 9}{3\sqrt{10}}=\frac{9}{\sqrt{10}};$

iuhj,

Треугольники $HXD$ и $PSD$ подобны, коэффициент подобия – $\frac{XD}{SD}=\frac{1}{3}.$ То есть $DH=\frac{PD}{3}=1$ , а $PH=2.$

Треугольники $PFH$ и $PRD$ подобны, коэффициент подобия – $\frac{PH}{PD}=\frac{2}{3}.$ Значит $FH=\frac{2RD}{3}=\frac{6}{\sqrt{10}}.$

Из прямоугольного треугольника $FHL:$

$FL=\sqrt{FH^2+HL^2}=\sqrt{(\frac{6}{\sqrt{10}})^2+6^2}=3\sqrt{\frac{22}{5}}.$

$cos\alpha=\frac{FH}{FL}=\frac{\frac{6}{\sqrt{10}}}{3\sqrt{\frac{22}{5}}}=\frac{1}{\sqrt{11}}.$

Далее, $S_{PHXCN}=S_{PDS}-S_{HXD}-S_{NCS}=\frac{27}{2}-\frac{3}{2}-\frac{3}{2}=\frac{21}{2}.$

Наконец, $S_{LKMNP}=\frac{S_{PHXCN}}{cos\alpha}=\frac{\frac{21}{2}}{\frac{1}{\sqrt{11}}}=\frac{21\sqrt{11}}{2}.$

Ответ: $\frac{21\sqrt{11}}{2}.$

Автор: egeMax | комментариев 5

Печать страницы

комментариев 5

Ранис

2014-12-26 в 20:40

В предпоследней строчке S pnxch , а не S pnxch

[ Ответить ]
- Ранис
  
  2014-12-26 в 20:41
  
  А не S phxch
  
  [ Ответить ]
  - egeMax
    
    2014-12-26 в 20:45
    
    Ранис, спасибо! Подправила.
    
    [ Ответить ]
Костя

2015-01-28 в 20:23

в пункте “б” я не понял, как находится CS=3, подскажите пжлст.

[ Ответить ]
- egeMax
  
  2015-01-28 в 23:45
  
  Треугольник $KMC_1$ равен треугольнику $SMC$ , ну а раз $KC_1=3$ , то и $SC=3.$
  
  [ Ответить ]

Задание №16 (С2) Т/Р №97 А. Ларина

Добавить комментарий Отменить ответ