Задание №16 Т/Р №101 А. Ларина

Смотрите также №15, №17, №18, №19, №20.
В прямоугольном параллелепипеде $ABCDA_1B_1C_1D_1$ известно, что $AB=8$, $BC=6,$ косинус угла между прямыми $BD$ и $AC_1$ равен $0,14$.
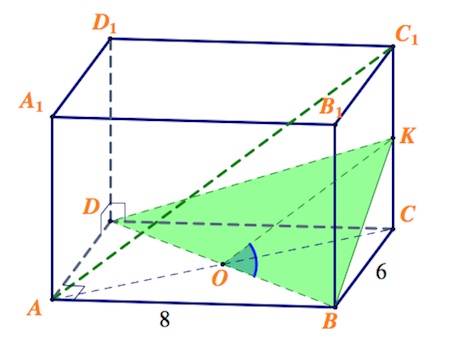
а) Постройте сечение параллелепипеда плоскостью, проходящей через точки $B$ и $D$ параллельно прямой $AC_1$.
б) Найдите объем пирамиды, отсекаемой от параллелепипеда этой плоскостью.

Решение:

a) Пусть $AC$ пересекается с $BD$ в точке $O$. Плоскость сечения пересекает плоскость $ACC_1$ по прямой (содержащей точку $O$), параллельной  $AC_1$. Пусть указанная прямая пересекается с ребром $CC_1$ в точке $K$.

Заметим (с учетом того, что $O$ – середина $AC$),  $K$ – середина $CC_1$ (по теореме о пропорциональных отрезках).

Треугольник $BKD$ – искомое сечение.

Уточним, косинус какого угла равен $0,14.$

Так как $OK\parallel AC_1$, то $\angle (AC_1;BD)=\angle (OK;BD)$.

Меньшим углом при пересечении прямых $BD, OK$ будет именно угол $KOB$ (угол $KOD$ – тупой ($|DK|>|BC|$)).

Итак, $cos\angle (AC_1;BD)=cos\angle BOK=0,14.$

б) $V_{BCDK}=\frac{1}{3}\cdot S_{BCD}\cdot  CK=\frac{1}{3}\cdot \frac{1}{2}\cdot 6\cdot 8\cdot CK=8CK.$

Наша задача – найти $CK.$

Пусть $CH\perp BD$. По теореме о трех перпендикулярах  и $KH\perp BD.$

Находим $CH$ из равнобедренного треугольника $BCO$ $(BO=OC=5, BC=6)$:

$CH\cdot BO=h_{BC}\cdot BC,$ где

$h_{BC}=\sqrt{BO^2-(\frac{BC}{2})^2}=4.$

Итак,

$CH=\frac{4\cdot 6}{5}=\frac{24}{5}.$

Из треугольника $OCH$ по т. Пифагора $HO=\sqrt{5^2-\frac{24^2}{25}}=\frac{7}{5}.$

Так как по условию $cosKOH=0,14$,  то   $\frac{OH}{OK}=0,14$. Откуда $OK=10.$

Из треугольника $OCK$  по т. Пифагора:

$KC=\sqrt{OK^2-OC^2}=\sqrt{100-25}=5\sqrt3.$

Итак,

$V_{BCDK}=8CK=8\cdot 5\sqrt3=40\sqrt3.$

Ответ: $40\sqrt3.$