Задание №16 Т/Р №103 А. Ларина

Смотрите также №15, №17, №18, №19, №20

Основанием пирамиды является равнобокая трапеция с основаниями 18 и 8. Каждая боковая грань пирамиды наклонена к основанию под углом $60^{\circ}$.

а) Докажите, что существует точка $O$, одинаково удаленная от всех граней пирамиды (центр вписанной сферы).
б) Найдите площадь полной поверхности данной пирамиды.

Решение:

a) Пусть $SN, SP, SQ, SM$ – апофемы граней $ABS, BCS, DCS$ и $ADC$ соответственно.

Тогда по т. о трех перпендикулярах $HN\perp AB,$ $HP\perp BC,$ $HQ\perp DC,$  $HM\perp AD$ (где $H$ – проекция вершины пирамиды на плоскость основнаия).

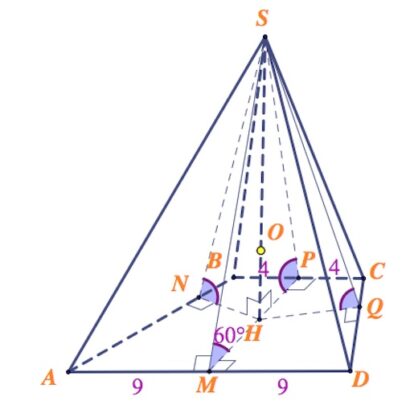
А поскольку треугольники $NHS,$  $PHS$,  $QHS$ и $MHS$ равны по катету и острому углу ($\angle SNH=…\angle SMH=60^{\circ}$), то $HN=HP=HQ=HM$. То есть $H$ – точка основания, равноудаленная от всех его сторон (центр вписанной окружности).

Плоскости $MHS$ и $ADS$ перпендикулярны по признаку перпендикулярности плоскостей, значит любой перпендикуляр плоскости $MHS$ к линии пересечения плоскостей, перпендикулярен $ADS$. Аналогично с остальными парами  плоскостей $ABS, NHS$; $BCS, PHS$; $DCS, QHS$.

Возьмем на прямой $HS$ такую точку $O$, что $OH=OT$, где $OT\perp MS$. Автоматически имеем,  что $O$ равноудалена от всех граней пирамиды, то есть является центром вписанной сферы.

б) Так как $H$ – центр вписанной окружности в основание пирамиды, то  по свойству отрезков касательных (с учетом того, что трапеция равнобедренная) $BP=PC=CQ=NB$ и $AM=MD=AN=DQ$.

Высота трапеции есть $\sqrt{13^2-5^2}$, то есть $12$.

Тогда из прямоугольного треугольника $MSH$ с углом в $60^{\circ}$ находим  $MS:$

$MS=2\cdot MH=12.$

Итак, находим площадь $S$ полной поверхности пирамиды

$S=S_{ABCD}+\frac{1}{2}\cdot P_{ABCD}\cdot MS=\frac{8+18}{2}\cdot 12+\frac{1}{2}\cdot 52\cdot 12=468.$

Ответ: 468.