Главная › 13 (С2) Стереометр. задачи › Задание №16 Т/Р №106 А. Ларина

26 Фев 2015

Категория: 13 (С2) Стереометр. задачиСтереометрияТ/P A. Ларина

Задание №16 Т/Р №106 А. Ларина

Елена Репина 2015-02-26 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №14»

Смотрите также №15, №17, №18, №19, №20.
В правильной четырехугольной призме $ABCDA_1B_1C_1D_1$ сторона основания равна $\sqrt2$ , а боковое ребро равно 2. Точка $M$ – середина ребра $AA_1$ . Найдите расстояние от точки $M$ до плоскости $DA_1C_1$ .

Решение:

Расстояние от $M$ до $DA_1C_1$ – есть длина высоты $h$ пирамиды $MDA_1C_1$ (основание – $DA_1C_1$ ).

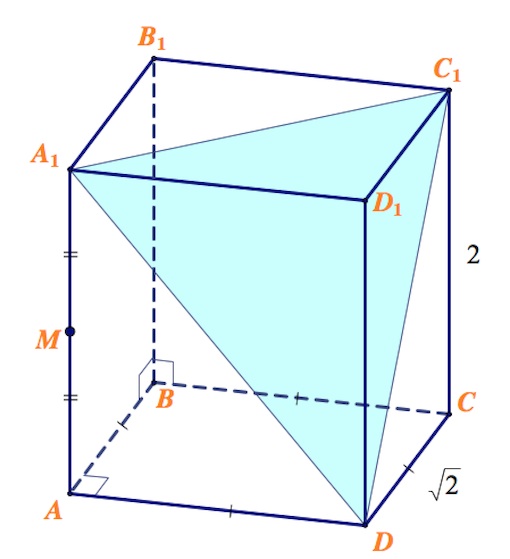
Найдем объем пирамиды $MDA_1C_1$ , но теперь уже беря в качестве основания грань $MA_1D$ . Заметим, $C_1D_1\perp MA_1D.$

$V=\frac{1}{3}S_{MA_1D}\cdot C_1D_1;$

$V=\frac{1}{3}(\frac{1}{2}A_1M\cdot AD)\cdot C_1D_1;$

$V=\frac{1}{3}\cdot \frac{1}{2}\cdot 1\cdot \sqrt2\cdot \sqrt2;$

$V=\frac{1}{3}.$

С другой стороны, $V=\frac{1}{3}S_{DA_1C_1}\cdot h.$

Найдем $S_{DA_1C_1}.$

Треугольник $A_1C_1D$ – равнобедренный с основанием $A_1C_1=2$ и высотой $DH$ , равной $\sqrt5.$

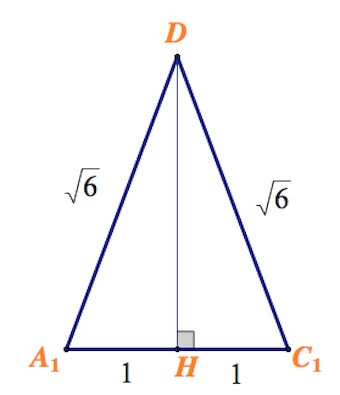
lkmlkm

$S_{DA_1C_1}=\frac{1}{2}\cdot 2\cdot \sqrt5=\sqrt5.$

Итак, c одной стороны $V=\frac{1}{3}$ , с другой $V=\frac{1}{3}\cdot \sqrt5\cdot h.$

Тогда

$\frac{1}{3}=\frac{1}{3}\cdot \sqrt5\cdot h;$

$h=\frac{\sqrt5}{5}.$

Ответ: $\frac{\sqrt5}{5}.$

Автор: egeMax | комментария 4

Печать страницы

комментария 4

Наталья

2015-03-17 в 22:01

как может равняться площадь MA1D=1\2A1M*AD
Это ведь не прямоугольный треугольник, к чему здесь эта формула?

[ Ответить ]
- egeMax
  
  2015-03-17 в 22:10
  
  A_1M – сторона, AD – высота. Надеюсь, вам известна формула площади через полупроизведение стороны на высоту, к ней проведенную?
  
  [ Ответить ]
  - Наталья
    
    2015-03-17 в 22:19
    
    Да, все верно, я не так прочла.
    Благодарю
    
    [ Ответить ]
    - egeMax
      
      2015-03-17 в 22:24
      
      ;)
      
      [ Ответить ]

Добавить комментарий Отменить ответ

Найти:
Материалы для подготовки к ЕГЭ
№12 №14 №15 №17
Рубрики
- 01 Геометрия (13)
- 02 Стереометрия (9)
- 03 Теория вероятностей ч.1 (1)
- 04 Теория вероятностей ч.2 (1)
- 05 Простейшие уравнения (5)
- 06 Вычисления (5)
- 07 Производная, ПО (4)
- 08 «Прикладные» задачи (5)
- 09 Текстовые задачи (7)
- 10 Графики функций (7)
- 11 Исследование функции (2)
- 12 (С1) Уравнения (78)
- 13 (С2) Стереометр. задачи (94)
- 14 (С3) Неравенства (89)
- 15 (С4) Практич. задачи (71)
- 16 (С5) Планиметр. задачи (86)
- 17 (С6) Параметры* (79)
- 18 (С7) Числа, их свойства (38)
- A1 Простейшие текст/задачи (нет в ЕГЭ-22) (3)
- A2 Читаем графики (нет в ЕГЭ-22) (1)
- Видеоуроки (44)
- ГИА (11)
  - II часть (11)
- ЕГЭ (диагностич. работы) (70)
- Иррациональные выражения, уравнения и неравенства (15)
- Логарифмы (39)
- МГУ (12)
- Метод интервалов (4)
- Метод рационализации (18)
- Модуль (9)
- Параметр (40)
- Переменка (5)
- Планиметрия (60)
- Показательные выражения, уравнения и неравенства (8)
- Разложение на множители (1)
- Рациональные выражения, уравнения и неравенства (10)
- Справочные материалы (92)
- Стереометрия (52)
- Т/P A. Ларина (443)
- Текстовые задачи (12)
- Теория чисел (2)
- Тесты по темам (80)
- Тригонометрические выражения, уравнения и неравенства (43)
- Функции и графики (10)
Дружественные сайты
Сайт А. Ларина ЕгэТренер – О. Себедаш Математика?Легко! Егэ? Ок! – И. Фельдман
Свежие записи
Архивы Архивы