Главная › 13 (С2) Стереометр. задачи › Задание №16 Т/Р №116 А. Ларина

07 Май 2015

Категория: 13 (С2) Стереометр. задачиСтереометрияТ/P A. Ларина

Задание №16 Т/Р №116 А. Ларина

Елена Репина 2015-05-07 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №14»

Смотрите также №15, №17, №18, №19, №20.

В прямоугольном параллелепипеде $ABCDA_1B_1C_1D_1$ $AB=BC=8$ , $BB_1=6$ . Точка $K$ – середина ребра $BB_1$ , точка $P$ – середина ребра $C_1D_1$ . Найдите:
а) площадь сечения параллелепипеда плоскостью, проходящей через точки $K$ и $P$ параллельно прямой $BD_1$ ;
б) объем большей части параллелепипеда, отсекаемой от него этой плоскостью.

Решение:

а) Плоскость сечения пересечет плоскость $BD_1B_1$ (в которой лежит $BD_1$ ) по прямой (содержащей точку $K$ ), параллельной $BD_1$ , так как $BD_1$ по условию параллельна плоскости сечения. Пусть указанная прямая (параллельная $BD_1$ , содержащая точку $K$ ) пересекается с $B_1D_1$ в точке $E$ ( $E$ – середина $B_1D_1$ ).

Пусть $PE$ пересекается с $A_1B_1$ в точке $L.$ Соединяем $L$ и $K$ . Проводим в плоскости $DCC_1$ через точку $P$ прямую, параллельную $LK$ (параллельные плоскости пересекаются третьей по параллельным прямым). Пусть последняя прямая пересекается с $CC_1$ в точке $T$ ( $T$ – середина $CC_1$ ).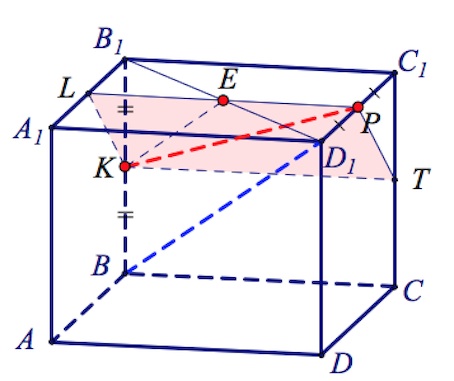

Параллелограмм $LPTK$ – искомое сечение.

А точнее, $LPTK$ – прямоугольник, так как $LP\parallel A_1D_1$ ( $P$ – середина $D_1C_1$ по условию, $E$ – центр $A_1B_1C_1D_1$ ), а $A_1D_1\perp AA_1B_1$ , то есть $A_1D_1\perp LK$ .

Очевидно, $LP=8,PT=\frac{D_1C}{2}=5.$

$S_{LPTK}=5\cdot 8=40.$

б) $V_{ABCDA_1B_1C_1D_1}=8\cdot 8\cdot 6.$

$V_{PC_1TLB_1K}=S_{PC_1T}\cdot LP=\frac{4\cdot 3}{2}\cdot 8=6\cdot 8.$

Тогда искомый объем есть $V_{ABCDA_1B_1C_1D_1}-V_{PC_1TLB_1K}=8\cdot 8\cdot 6-6\cdot 8=48(8-1)=336.$

Ответ:

а) 40.

б) 336.

Автор: egeMax | комментариев 12

Печать страницы

комментариев 12

Марат

2015-05-11 в 19:01

Почему E – середина B1D1?

[ Ответить ]
- egeMax
  
  2015-05-11 в 20:36
  
  Мы проводили KE параллельно BD1. Раз K – середина BB1, то и E – середина B1D1 по теореме о пропорциональных отрезках:
  Параллельные прямые, пересекающие стороны угла, отсекают от его сторон пропорциональные отрезки
  
  [ Ответить ]
  - Марат
    
    2015-05-12 в 05:57
    
    Теорема Фалеса?
    
    [ Ответить ]
    - egeMax
      
      2015-05-12 в 07:49
      
      Да, следствие из нее.
      
      [ Ответить ]
Валерия

2016-02-10 в 21:29

Как может быть плоскость параллельна ВD1? И КР параллельна BD1 ??

[ Ответить ]
- egeMax
  
  2016-02-10 в 21:36
  
  1) Прямая параллельна плоскости, если в плоскости найдется прямая, ей параллельная.
  BD1 параллельна KE, значит ВD1 параллельна плоскости, содержащей KE.
  2) KP НЕ параллельна BD1. Откуда вы это взяли?
  
  [ Ответить ]
Вика

2016-04-06 в 16:20

Елена Юрьевна, помогите!
В прямоугольном параллепипеде АВСДА1В1С1Д1 известны длины ребер АА1=7, АВ=16, АД=6. Точка К -середина ребра С1Д1.
а) Докажите, что плоскость, переходящая через точку В перпендикулярно прямой АК, пересекает отрезок А1К1.
б) Найдите тангенс угла между этой плоскостью и плоскостью АВС.

[ Ответить ]
- egeMax
  
  2016-04-06 в 21:15
  
  Тангенс угла между этой плоскостью и плоскостью ABC – есть тангенс угла между нормалями к плоскостям. Нормаль к ABC – AA_1, например; нормаль к указанной плоскости – AK. Тангенс угла тогда есть 10/7.
  В пункте a не понятно, откуда у вас взялась точка K_1… вы не описали…
  
  [ Ответить ]
Игнат

2016-05-05 в 14:26

В прямоугольном параллелепипеде АВСDA1B1C1D1 известны длины ребер: АА1=7, АВ=16, AD=6. Точка К — середина ребра С1D1. Докажите, что плоскость, проходящая через т B перпендикулярно прямой AK пересекает отрезок A1K. Елена Юрьевна, подскажите пожалуйста как решить

[ Ответить ]
- egeMax
  
  2016-05-05 в 15:27
  
  Саму плоскость-то построили?
  
  [ Ответить ]
  - Ольга
    
    2016-07-02 в 13:10
    
    ПОДСКАЖИТЕ КАК СТРОИТЬ СЕЧЕНИЯ
    
    [ Ответить ]
    - egeMax
      
      2016-07-02 в 21:47
      
      Как строить ВООБЩЕ? В двух словах не могу подсказать.
      Как строить конкретно в данной задаче – вроде рассказала.
      Посмотрите построение сечений здесь, здесь, здесь, здесь, здесь, здесь, здесь, здесь…
      
      [ Ответить ]

Задание №16 Т/Р №116 А. Ларина

Добавить комментарий Отменить ответ