Главная › 13 (С2) Стереометр. задачи › Задание №16 Т/Р №120 А. Ларина

01 Июн 2015

Категория: 13 (С2) Стереометр. задачиСтереометрияТ/P A. Ларина

Задание №16 Т/Р №120 А. Ларина

Елена Репина 2015-06-01 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №14»

Смотрите также №15, №17, №18, №19, №20.

В правильной треугольной пирамиде $PABC$ ( $ABC$ – основание) $M$ – точка пересечения медиан грани $PBC$ .
a) Докажите, что прямая $AM$ делит высоту $PO$ пирамиды в отношении $3:1$ , считая от точки $P$ .
б) Найдите объем многогранника с вершинами в точках $A$ , $B$ , $M$ , $P$ , если известно, что $AB=12$ , $PC=10$ .

Решение:

а) Пусть $O$ – центр основания (точка пересечения медиан $\Delta ABC$ ).

Очевидно (по свойству медиан треугольника), $AO:ON=2:1$ ( $N$ – середина $BC$ ).

При этом $AN=\sqrt{12^2-6^2}=6\sqrt3.$

Тогда $AO=4\sqrt3,$ $ON=2\sqrt3.$

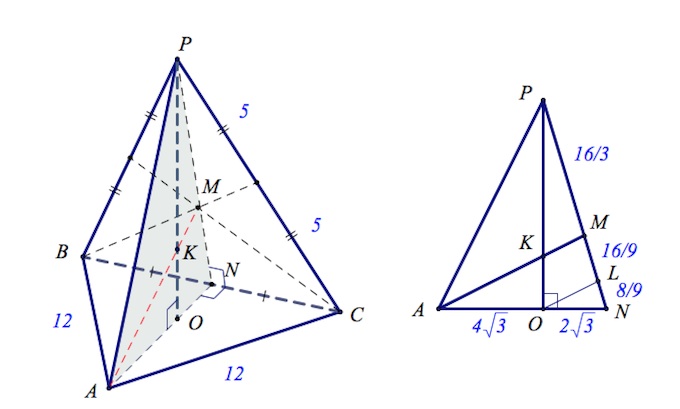
Заметим, что (опять же, по свойству медиан) $PM:MN=2:1$ .

При этом $PN=8$ (по т. Пифагора из $\Delta PCN$ ).

Тогда $PM=\frac{16}{3},$ $MN=\frac{8}{3}.$

Проведем $OL$ параллельно $AM$ ( $L\in PN$ ).

По теореме о пропорциональных отрезках $AO:ON=ML:LN$ , поэтому $ML:LN=2:1$ . С учетом того, что $MN=\frac{8}{3}$ имеем $ML=\frac{16}{9},$ $LN=\frac{8}{9}.$

Опять же по теореме о пропорциональных отрезках $PK:KO=PM:ML=\frac{\frac{16}{3}}{\frac{16}{9}}=3:1.$

Итак, $PK:KO=3:1.$ Что и требовалось доказать.

б) Будем рассматривать многогранник с вершинами в точках $A,B,M,P$ как пирамиду с основанием $AMP$ и вершиной $B$ .

Причем заметим, что $BN$ – высота пирамиды ( $BN\perp (APN)$ ).

По тореме косинусов для $\Delta APN:$

$AN^2=AP^2+NP^2-2AP\cdot NP\cdot cosP;$

$cosP=\frac{100+64-36\cdot 3}{2\cdot 10\cdot 8};$

$cosP=\frac{7}{20};$

Тогда $sin P=\frac{\sqrt{351}}{20}=\frac{3\sqrt{39}}{20}.$

$S_{AMP}=\frac{1}{2}\cdot AP\cdot PM\cdot sinP=\frac{1}{2}\cdot 10\cdot \frac{16}{3}\cdot \frac{3\sqrt{39}}{20}=4\sqrt{39}.$

$V_{AMPB}=\frac{1}{3}\cdot S_{APM}\cdot BN=8\sqrt{39}.$

Ответ: $8\sqrt{39}.$

Автор: egeMax | комментариев 7

Печать страницы

комментариев 7

Sasha

2015-06-01 в 11:44

Обычно когда решаешь пункт А не нужно использовать данные из пункта Б.

[ Ответить ]
- egeMax
  
  2015-06-01 в 12:07
  
  Да, безусловно. Но ведь все равно нам для выполнения пункта б придется делать вычисления. Так что…
  
  [ Ответить ]
ганс

2015-06-01 в 13:39

крутяк

[ Ответить ]
Михаил

2015-06-02 в 05:57

правильный ответ 16 корней из 39

[ Ответить ]
- egeMax
  
  2015-06-02 в 08:45
  
  Нет, правильный ответ $8\sqrt{39}.$
  
  [ Ответить ]
Андрей

2015-06-02 в 14:31

здравствуйте) можно было проще доказать первый пункт: по формуле( PK/KO=PM/MN(1+NO/AO)

[ Ответить ]
- egeMax
  
  2015-06-02 в 15:33
  
  Да, для тех, кто знает теорему Менелая.
  
  [ Ответить ]

Задание №16 Т/Р №120 А. Ларина

Добавить комментарий Отменить ответ