Задание №16 Т/Р №210 А. Ларина

Смотрите также №13; №14; №15; №17; №18; №19 Тренировочной работы №210 А. Ларина.

16. В равнобедренной трапеции $ABCD$ основание $AD$ в два раза больше основания $BC.$

а) Докажите, что высота $CH$ трапеции разбивает основание $AD$ на отрезки, один из

которых втрое больше другого.
б) Пусть $O$ — точка пересечения диагоналей трапеции $ABCD$. Найдите расстояние от вершины $C$ до середины отрезка $OD$, если $BC=16$ и $AB=10$.

Решение:

a) Проведем $CK\parallel AB,$ ($K\in (AD)$).

Тогда $ABCK$ – параллелограмм и $CK=AB.$ А поскольку по условию $AB=CD,$ то и $KC=CD.$

В равнобедренном треугольнике $KCD$ высота $CH$ является и медианой.

Учитывая, что $BC=AK=KD$ , получаем, что

$HD=\frac{KD}{2}=\frac{\frac{AD}{2}}{4}=\frac{AD}{4},$

$AH=\frac{3AD}{4}.$

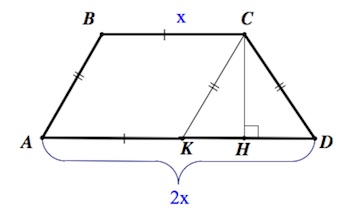
Итак, высота $CH$ делит основание $AD$ на отрезки, один из которых втрое больше другого.

Что и требовалось доказать.

б) Пусть $BQ$ – также высота трапеции. Пусть $CH$ пересекается с $BD$ в точке $M.$

Треугольники $BDQ,MDQ$ подобны по двум углам и коэффициент подобия их – $\frac{HD}{QD}=1:3.$

Но тогда и $MD:BD=1:3$

Заметим также, что треугольники $BCO,DAO$ подобны и коэффициент подобия их – $\frac{BC}{AD}=1:2.$

Но тогда $OD=2BO.$

Итак, $BO=OM=MD.$

То есть $M$ – середина $OD$ и нам необходимо найти $CM=CH-HM=CH-\frac{CH}{3}=\frac{2CH}{3}.$

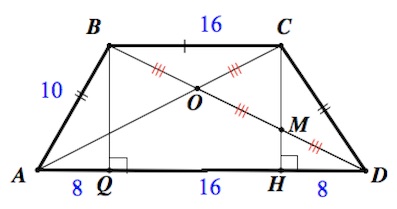
Несложно понять, что высота данной трапеции равна $6$, а потому $CM=4.$

Ответ: б) $4.$