Задание №16 Т/Р А. Ларина

Смотрите также №15, №17, №18, №19, №20.

Ребро куба $ABCDA_1B_1C_1D_1$ равно 12. Точка $P$ – середина ребра $CB$, точка $K$ лежит на ребре $CD$ так, что $KD:KC=1:2$. Плоскость, проходящая через точки $P$, $K$ и $A_1$ пересекает ребро $DD_1$ в точке $M$.
а) Докажите, что$ DM:D_1M=1:4$.
б) Найдите угол между плоскостями $PKA_1$ и $ABC$.

Решение:

a) Пусть $PK$ пересекается с $AD$ в точке $L$.

$LA_1$ пересекается с $DD_1$ в точке $M.$

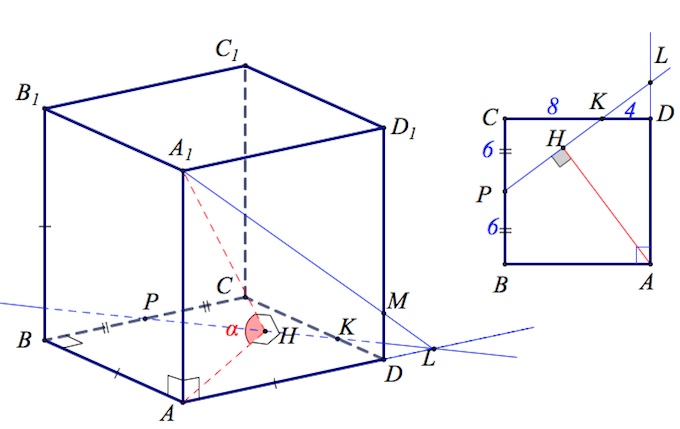
Треугольники $PCK,$   $LDK$  подобны, $k=\frac{CK}{DK}=2.$

Тогда $DL=\frac{PC}{2}=3.$

Треугольники $LDM,$   $A_1D_1M$  подобны, $k=\frac{LD}{A_1D_1}=\frac{1}{4}.$  Но тогда и $DM:D_1M=1:4$.

Что и требовалось доказать.

б) $PK$ – прямая пересечения плоскостей $PKA_1, ABC.$

Пусть $AH\perp PK$. По теореме о трех перпендикулярах  и $A_1H\perp PK$. То есть $\alpha=\angle AHA_1$ – угол между плоскостями $PKA_1, ABC.$

Треугольники $AHL,$  $KDL$  подобны, $k=\frac{AL}{KL}=\frac{15}{5}=3.$ Тогда $AH=3KD=12.$

Итак, в треугольнике $AHA_1$ катеты $AH, AA_1$ равны, что означает, что угол $\alpha$ равен $45^{\circ}.$

Ответ: б) 45.