Задание №17 (С3) Т/Р №94 А. Ларина

Смотрите также №15, №16, №18, №19, №20.

Решите неравенство:

$\frac{log_5(x^2-4x-11)^2-log_{11}(x^2-4x-11)^3}{2-5x-3x^2}\geq 0.$

Решение:

a) Отдельно рассмотрим случай: $x^2-4x-11=1.$

В этом случае $x=-2$ или $x=6$, но только $x=6$ удовлетворяет неравенству.

б) Далее рассматриваем $x^2-4x-11\neq 1.$

Для краткости, временно, обозначим $x^2-4x-11$ за $m$ и поработаем с разностью $log_5(x^2-4x-11)^2-log_{11}(x^2-4x-11)^3:$

$log_5m^2-log_{11}m^3=2log_5m-3log_{11}m=\frac{2}{log_m5}-\frac{3}{log_m11}=\frac{2log_m11-3log_m5}{log_m5\cdot log_m11}=$

$=\frac{log_m121-log_m125}{log_m5\cdot log_m11}=\frac{log_m\frac{121}{125}}{log_m5\cdot log_m11}=\frac{log_5\frac{121}{125}}{log_m11}.$

Так как  $log_5\frac{121}{125}<log_51$,  то  $log_5\frac{121}{125}<0$, то есть знак разности $log_5m^2-log_{11}m^3$  –  есть знак    $-log_m11.$

Итак, в случае $x\neq 6$ исходное неравенство равносильно следующему:

$\frac{-\log_{(x^2-4x-11)}11}{2-5x-3x^2}\geq 0.$

Далее

$log_{(x^2-4x-11)}11\cdot (3x-1)(x+2)\geq 0,$  $x\neq \frac{1}{3}, x\neq -2;$

Знак   $log_{(x^2-4x-11)}11$,  согласно методу рационализации, есть знак

$(x^2-4x-11-1)(11-1)$   на $x^2-4x-11>0$.

Итак, перед нами система:

$\begin{cases}(x^2-4x-12)(3x-1)(x+2)\geq 0,\\x^2-4x-11>0,\\x\neq \frac{1}{3},\\x\neq -2;\end{cases}$

$\begin{cases}(x-6)(3x-1)(x+2)^2\geq 0,\\(x-(2-\sqrt{15}))(x-(2+\sqrt{15}))>0,\\x\neq \frac{1}{3},\\x\neq -2;\end{cases}$

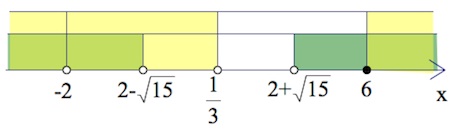
Учитывая (а) и (б), имеем:

$x\in (-\infty;-2)\cup (-2;2-\sqrt{15})\cup [6;+\infty).$

Ответ: $(-\infty;-2)\cup (-2;2-\sqrt{15})\cup [6;+\infty).$