Главная › 14 (С3) Неравенства › Задание №17 (С3) Т/Р №95 А. Ларина

11 Дек 2014

Категория: 14 (С3) НеравенстваЛогарифмыМетод рационализацииТ/P A. Ларина

Задание №17 (С3) Т/Р №95 А. Ларина

Елена Репина 2014-12-11 2016-02-10

В новом формате ЕГЭ по математике задание значится как «Задание №15»

Смотрите также №15, №16, №18, №19, №20.

Решите неравенство: $log_xlog_2(3-4^{x-1})\leq 1.$

Решение:

Решаем методом рационализации (методом замены множителей).

$\begin{cases} (x-1)(log_2(3-4^{x-1})-x)\leq 0,& &x>0,& &x\neq 1,& &log_2(3-4^{x-1})>0;& \end{cases}$

И опять применяем метод замены множителей к $log_2(3-4^{x-1})-x:$

$\begin{cases} (x-1)(3-4^{x-1}-2^x)\leq 0,& &x>0,& &x\neq 1,& &3-4^{x-1}>1;& \end{cases}$

$\begin{cases} (x-1)((2^{x})^2+4\cdot 2^x-12)\geq 0,& &x>0,& &x\neq 1,& &4^{x-1}<2;& \end{cases}$

$\begin{cases} (x-1)(2^{x}-2)(2^x+6)\geq 0,& &x>0,& &x\neq 1,& &2^{2x-2}<2;& \end{cases}$

И опять применяем метод замены множителей к $2^{x}-2$ первой строки системы (знак $2^x+6$ – плюс – «откидываем» множитель):

$\begin{cases} (x-1)(x-1)\geq 0,& &x>0,& &x\neq 1,& &2x-2<1;& \end{cases}$

$\begin{cases} (x-1)^2\geq 0,& &x>0,& &x\neq 1,& &x<1,5;& \end{cases}$

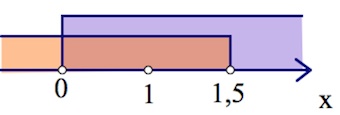
Ответ: $(0;1)\cup (1;1,5).$

Автор: egeMax | Нет комментариев

Печать страницы

Добавить комментарий Отменить ответ

Найти:
Материалы для подготовки к ЕГЭ
№12 №14 №15 №17
Рубрики
- 01 Геометрия (12)
- 02 Стереометрия (9)
- 03 Теория вероятностей ч.1 (1)
- 04 Теория вероятностей ч.2 (1)
- 05 Простейшие уравнения (5)
- 06 Вычисления (5)
- 07 Производная, ПО (4)
- 08 «Прикладные» задачи (5)
- 09 Текстовые задачи (7)
- 10 Графики функций (7)
- 11 Исследование функции (2)
- 12 (С1) Уравнения (79)
- 13 (С2) Стереометр. задачи (95)
- 14 (С3) Неравенства (90)
- 15 (С4) Практич. задачи (72)
- 16 (С5) Планиметр. задачи (87)
- 17 (С6) Параметры* (80)
- 18 (С7) Числа, их свойства (39)
- A1 Простейшие текст/задачи (нет в ЕГЭ-22) (3)
- A2 Читаем графики (нет в ЕГЭ-22) (1)
- Видеоуроки (44)
- ГИА (11)
  - II часть (11)
- ЕГЭ (диагностич. работы) (70)
- Задачи (34)
- Иррациональные выражения, уравнения и неравенства (15)
- Логарифмы (39)
- МГУ (12)
- Метод интервалов (4)
- Метод рационализации (18)
- Модуль (9)
- Параметр (40)
- Переменка (5)
- Планиметрия (59)
- Показательные выражения, уравнения и неравенства (8)
- Разложение на множители (1)
- Рациональные выражения, уравнения и неравенства (10)
- Справочные материалы (94)
- Стереометрия (52)
- Т/P A. Ларина (443)
- Текстовые задачи (12)
- Теория чисел (2)
- Тесты по темам (80)
- Тригонометрические выражения, уравнения и неравенства (43)
- Функции и графики (10)
Дружественные сайты
Сайт А. Ларина ЕгэТренер – О. Себедаш Математика?Легко! Егэ? Ок! – И. Фельдман
Свежие записи
Архивы Архивы