Главная
Справочник
Видеоуроки
ЕГЭ
МГУ
Тесты
Карта сайта
Контакты
Смотрите также №15, №16, №18, №19, №20
Решите неравенство
$log_x(3-x)log_x(4-x)-log_x(x^2-7x+12)+1\geq 0.$
Решение:
$log_x(3-x)log_x(4-x)-log_x((x-4)(x-3))+1\geq 0;$
$log_x(3-x)log_x(4-x)-log_x(4-x)-log_x(3-x)+1\geq 0;$
$log_x(3-x)(log_x(4-x)-1)-(log_x(4-x)-1)\geq 0;$
$(log_x(4-x)-1)(log_x(3-x)-1)\geq 0;$
Применяем метод замены множителей:
$\begin{cases}(x-1)(4-x-x)(x-1)(3-x-x)\geq 0,\\x>0,\\x\neq 1,\\4-x>0,\\3-x>0,&\end{cases}$
$\begin{cases}(x-1)^2(4-2x)(3-2x)\geq 0,\\x>0,\\x\neq 1,\\x<3;&\end{cases}$
$\begin{cases}(x-1)^2(x-2)(x-1,5)\geq 0,\\x\neq 1,\\0<x<3;&\end{cases}$
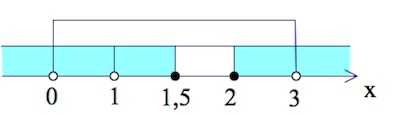
$x\in (0;1)\cup (1;1,5]\cup [2;3).$
Ответ: $(0;1)\cup (1;1,5]\cup [2;3).$
Объясните пожалуйста решение: почему во второй строке решения были поменяны знаки выражений под знаком логарифма, при этом знак неравенства был сохранён, а после применения метода рационализации знак неравенства поменяли?
Иван, смотрите.
[latexpage]$(x-3)(x-4)$ есть $(3-x)(4-x)$, верно?
Но первое слагаемое $log_x9(3-x)log_x(4-x)$ не позволяет ‘расщепить’ второе на $log_x(x-3)+log_x(x-4)$, ведь иначе подлогарифмические выражения отрицательны.
Нужно понимать, что, вообще говоря, $log_axy$ не есть всегда $log_ax+log_ay$ (это верно лишь в случае $x,y>0$). Может быть и так: $log_axy=log_a(-x)+log_a(-y)$ (при $x,y<0$).
После применения метода рационализации знак был изменен ввиду опечатки...
спасибо, теперь понятно )
Объясните пожалуйста, как в решении получили 4 и 5 строчки?
Анастасия, в 4-й строке вынесли общий множитель [latexpage] $(log_x(4-x)-1)$ за скобку.
В 5-й применили метод замены множителей (ссылка указана при решении).
Обращайтесь, если что еще непонятно…
мне непонятно, почему промежуток от 0 до 1 вошел в ответ.
Исходя из решения…
Где именно возникло непонимание?
Почему как одз рассматривается 3-x>0 и 4-x>0, а не (x^2-7x+12)>0??
Дмитрий, ограничение 3-x>0 и 4-x>0 диктует нам первое слагаемое неравенства. Против этого не попрешь.
При этом x^2-7x+12=(3-x)(4-x). Замечаем, что x^2-7x+12>0 в двух случаях:
3-x>0 и 4-x>0
или
3-x<0 и 4-x<0.
Так?
Второй случай невозможен, так как первое слагаемое неравенства тогда перестает существовать.
Понятно ли так?
Да-да, я чуть позже понял. Спасибо:)
Каким образом в 5-ой строке применён метод замены множителей, что происходит с минус 1, она заменяется логарифмом? распишите это подробно, пожалуйста.
Ирина, [latexpage] знак $log_x(4-x)-1$ (или что тоже самое – $log_x(4-x)-log_xx$) совпадает со знаком произведения $(x-1)(4-x-x)$ на ОДЗ.
А откуда получилось (х—1) после замены
Из основания (логарифма), то есть из x, вычли 1. Чтобы понять, нужно изучить метод замены множителей, он же – метод рационализации.