Задание №17 Т/Р №106 А. Ларина

Смотрите также №15, №16, №18, №19, №20.

Решите неравенство

$\large log_{4x}2x-log_{2x^2}4x^2\geq -\frac{3}{2}.$

Решение:

$\large\frac{log_22x}{log_24x}-\frac{log_24x^2}{log_22x^2}\geq -\frac{3}{2};$

$\large\frac{1+log_2x}{2+log_2x}-\frac{2+2log_2x}{1+2log_2x}\geq -\frac{3}{2};$

$\large\frac{2(1+log_2x)(1+2log_2x)-2(2+2log_2x)(2+log_2x)+3(2+log_2x)(1+2log_2x)}{2(2+log_2x)(1+2log_2x)}\geq 0;$

$\large\frac{2+6log_2x+4log^2_2x-8-12log_2x-4log^2_2x+6+15log_2x+6log^2_2x}{2(2+log_2x)(1+2log_2x)}\geq 0;$

$\large\frac{6log^2_2x+9log_2x}{2(2+log_2x)(1+2log_2x)}\geq 0;$

$\large\frac{log_2x(log_2x+\frac{3}{2})}{(2+log_2x)(\frac{1}{2}+log_2x)}\geq 0;$

(применяем метод замены множителей)

$\large\frac{(x-1)(x-\frac{1}{\sqrt8})}{(x-\frac{1}{4})(x-\frac{1}{\sqrt2})}\geq 0$ при условии $x>0.$

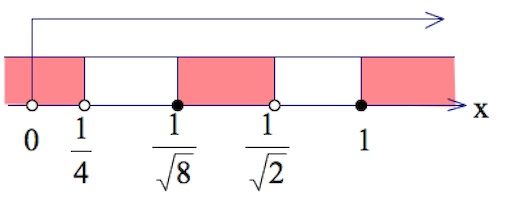
$x\in (0;\frac{1}{4})\cup [\frac{1}{\sqrt8};\frac{1}{\sqrt2})\cup [1;+\infty).$

Ответ: $(0;\frac{1}{4})\cup [\frac{1}{\sqrt8};\frac{1}{\sqrt2})\cup [1;+\infty).$