Главная
Справочник
Видеоуроки
ЕГЭ
МГУ
Тесты
Карта сайта
Контакты
Смотрите также №15, №16, №18, №19, №20
Решите неравенство:
$log_{5-x}(5+9x-2x^2)+log_{1+2x}(x^2-10x+25)^2\leq 5.$
Решение:
$log_{5-x}(5-x)(1+2x)+log_{1+2x}(5-x)^4\leq 5;$
$1+log_{5-x}(1+2x)+4log_{1+2x}(5-x)\leq 5;$
$1+log_{5-x}(1+2x)+\frac{4}{log_{5-x}(1+2x)}\leq 5;$
$\frac{log^2_{5-x}(1+2x)-4log_{5-2x}(1+2x)+4}{log_{5-x}(1+2x)}\leq 0;$
$\frac{(log_{5-x}(1+2x)-2)^2}{log_{5-x}(1+2x)}\leq 0;$
Применяем метод рационализации (метод замены множителей):
$\begin{cases}\frac{((5-x-1)(1+2x-(5-x)^2))^2}{(5-x-1)(1+2x-1)}\leq 0,\\5-x>0,\\5-x\neq 1,\\1+2x>0,\\1+2x\neq 1;&\end{cases}$
$\begin{cases}\frac{(4-x)^2(x^2-12x+24)^2}{x(4-x)}\leq 0,\\x<5,\\x\neq 4,\\x>-\frac{1}{2},\x\neq 0;&\end{cases}$
$\begin{cases}\frac{(4-x)(x-(6-2\sqrt3))^2(x-(6+2\sqrt3))^2}{x}\leq 0,\\x<5,\\x\neq 4,\\x>-\frac{1}{2},\x\neq 0;&\end{cases}$
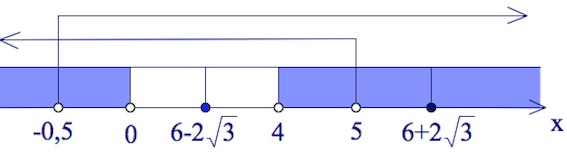
Ответ: $(-0,5;0)\cup${$6-2\sqrt3$}$\cup (4;5).$
1) Для простоты записи полезно ввести замену. 2) Зачем же метод рационализации (из пушки по воробьям)? Числитель дроби равен нулю, знаменатель меньше нуля.
Татьяна Евгеньевна,
1) Не думаю, что отсутствие замены сильно усложнило решение… Ради трех строк?.. Крайне редко к ней прибегаю… Так уж повелось.. Только в случае явной необходимости использую.
2) Люблю рациональзацию! Естественно, видела ваш вариант (числитель дроби равен нулю, знаменатель меньше нуля) при решении, но остановилась именно на этом способе решения по двум причинам: а) честно говоря, было лень (бывает и такое…) искать/вставлять формулу скобки равносильности, – не хилый там набор значков неведомых… ; б) такое решение имеет место быть и не является топтанием на месте.