Смотрите также №15, №16, №18, №19, №20.
Решите неравенство $\large \frac{log_{(-36x)}6^{x+2}}{log_{36}6^{x+2}}\leq \normalsize log_{x^2}36.$
Решение:
$\large \frac{log_{(-36x)}6^{x+2}}{log_{36}6^{x+2}}\leq \normalsize log_{x^2}36;$
$\\$
$\Large \frac{\frac{1}{log_{6^{x+2}}(-36x)}}{\frac{1}{log_{6^{x+2}}36}}\leq \normalsize log_{|x|}6;$
$\\$
$\large \frac{log_{6^{x+2}}36}{log_{6^{x+2}}(-36x)}\leq \normalsize log_{(-x)}6;$
$\\$
$ log_{(-36x)}36\leq log_{(-x)}6$, $6^{x+2}\neq 1;$
$\\$
$\large \frac{2}{log_{6}36+log_{6}(-x)}\leq \frac{1}{log_{6}(-x)}$, $x\neq -2;$
$\\$
$\Large \frac{2}{2+log_{6}(-x)}\leq \frac{1}{log_{6}(-x)}$, $x\neq -2;$
$\\$
$\large \frac{2log_{6}(-x)-2-log_{6}(-x)}{(2+log_{6}(-x))log_{6}(-x)}\leq 0$, $x\neq -2;$
$\\$
$\large \frac{log_{6}(-x)-2}{(log_{6}(-x)-(-2))log_{6}(-x)}\leq 0$, $x\neq -2;$
К левой части неравенства применяем метод замены множителей:
$\begin{cases}\large \frac{-x-36}{(-x-\frac{1}{36})(-x-1)}\geq 0,\\x\neq -2,\\-x>0;&\end{cases}$
$\begin{cases}\large \frac{x+36}{(x+\frac{1}{36})(x+1)}\geq 0,\\x\neq -2,\\x<0;&\end{cases}$
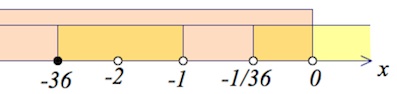
Ответ: $[-36;-2)\cup (-2;-1)\cup (-\frac{1}{36};0).$


Извините, почему в ответ не включён промежуток (-1; -1/36)?
Павел, а где основания, чтобы его включить в ответ? Откуда он у вас вылезает?
ОДЗ:
{
x < 0
x неравен -1/36
х неравен +- 1
x неравен -2
}
Перехожу к другому основанию: log-36x(6^x+2)=log36(6^x+2)/log36(-36x)
log36(6^x+2)/log36(-36x) * 1/log36(6^x+2) <= 1/log36(x^2)
1/log36(-36x) = log36(x^2) # обе части в -1 степень
-36x >= x^2
x^2 + 36x <= 0
x(x + 36) <= 0
Методом интервалов нахожу x E [-36; 0]. По ОДЗ выкалываю точки {0,-1, -2, -1/36}
Получаю x E [-36; -2) U (-2; -1) U (-1; -1/36) U (-1/36; 0)
[latexpage]Павел, ошибка у вас пошла при переходе от
$\frac{1}{log_{36}(-36x)}\leq \frac{1}{loq_{36}x^2}$
к
$log_{36}(-36x)\geq loq_{36}x^2.$
Нет здесь равносильного перехода!
Так надо далее действовать:
$\frac{loq_{36}x^2-log_{36}(-36x)}{log_{36}(-36x)\cdot loq_{36}x^2}\leq 0;$
Вы же не решаете, надеюсь, например, такое неравенство $\frac{1}{x}>1$ вот так: $x>1$?
Ведь надо так: $\frac{1-x}{x}>0$, откуда $x\in (0;1),$ а не $x\in (1;+\infty).$
Благодарю.
Хочу ещё уточнить два момента, оба о методе рационализации. Ваши примеры, решенные им, все ли имеют альтернативные решения?
Как относятся проверяющие к подобному методу?
Конечно, можно всегда обходиться без метода рационализации. Он лишь укорачивает путь (чаще всего). Эксперты его, конечно, должны знать. Если, вдруг, попадется проверяющий, не знакомый с ним, в чем сомневаюсь, и зарубит решение, то всегда можно подать на апелляцию. Но очень не советую применять рационализацию, если нет понимания сути происходящего!
Все равно не понимаю, почему этот промежуток не входит, объясните пожалуйста поподробнее
Анастасия, о каком промежутке идет речь? Не понимаю.
(-1; -1/36)
Почитайте диалог с Павлом. Как раз то, что вам нужно.
При решении неравенства 1/х<1 вы серьёзно думаете, что решением является промежуток от 0 до 1 ????????
А вам не кажется, что решением является два промежутка (-бесконечность;0)и (1;+бесконечность)
Очепатка. Спасибо!
Знак неравенства исправлен. При наборе эти знаки сложно вводить, словами прописываются, – осталась незамечена ошибка
Здравствуйте)))
объясните, пожалуйста, переход
\frac{log_{6^{x+2}}36}{log_{6^{x+2}}(-36x)}\leq log_{(-x)}6;
log_{(-36x)}36\leq log_{(-x)}6, 6^{x+2}\neq 1; я не поняла по каким свойствам логарифма это сделали.
P.S. На реальном егэ тоже могут попасться такие сложные неравенства???
[latexpage]Наталья, применено вот такое свойство логарифмов:
$\frac{log_ab}{log_ac}=log_cb$
Данное неравенство типично для заданий №17.
Можно вопросик?)
Почему Вы так упорно избегайте замены в 17-ой задаче?
Да уж, не впервые мне такой вопрос задается…
Так уж повелось… Не люблю ее делать. Прибегаю к ней в крайних случаях.
Елена, если начать решение с области допустимых значений для переменной х, то детям, я думаю (показывает моя статистика), было бы проще читать и понимать решение.
С уважением, Елена.
Но ведь случается, – рассматривая допустимые значения для переменной, мы делаем лишнюю работу. Нет-нет, да васкакивает какое-нибудь неравенство, например, которое можно было бы и не решать, идя через равносильность.
Поэтому не могу заставить себя решать через ОДЗ :(
И приучаю детей к равносильным переходам. Да, бывают случаи, когда выгоднее начать с одз.
Елена, спасибо за коммент!
Спасибо, Елена. Попробую подействовать также.Возможно есть большие плюсы…
Объясните пожалуйста откуда берется минус в основании логарифма и еще не совсем ясно откуда берется 2 в числителе
1) [latexpage]Дима, $|x|=-x$ при $x<0$. У нас именно такой случай согласно ОДЗ.
2) $log_{(-36x)}36=log_{(-36x)}6^2=2log_{(-36x)}6=\frac{2}{log_6(-36x)}.$
Имею в виду это (-х)