Главная › 14 (С3) Неравенства › Задание №17 Т/Р №120 А. Ларина

01 Июн 2015

Категория: 14 (С3) НеравенстваЛогарифмыТ/P A. Ларина

Задание №17 Т/Р №120 А. Ларина

Елена Репина 2015-06-01 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №15»

Смотрите также №15, №16, №18, №19, №20.

Решите неравенство $log_x(11x-2x^2)+log_{11-2x}x^4\leq 5.$

Решение:

$log_x(11x-2x^2)+log_{11-2x}x^4\leq 5;$

$log_xx+log_x(11-2x)+\frac{1}{log_{x^4}11-2x}\leq 5;$

$1+log_x(11-2x)+\frac{4}{log_{|x|}(11-2x)}\leq 5;$

$\frac{log^2_x(11-2x)-4log_x(11-2x)+4}{log_{x}(11-2x)}\leq 0;$

$\frac{(log_x(11-2x)-2)^2}{log_{x}(11-2x)}\leq 0;$

Применяем метод замены множителей:

$\begin{cases} \frac{((x-1)(11-2x-x^2))^2}{(x-1)(11-2x-1)}\leq 0,& &x>0,& &x\neq 1,& &11-2x>0;& \end{cases}$

$\begin{cases} \frac{(x-1)(x-(-1+2\sqrt{3}))^2(x-(-1-2\sqrt{3}))^2}{10-2x}\leq 0,& &x>0,& &x\neq 1,& &x<5,5;& \end{cases}$

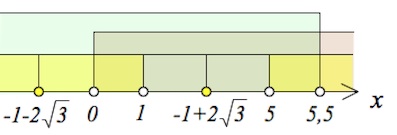
Ответ: $(0;1)\cup$ { $-1+2\sqrt3$ } $(5;5,5).$

Автор: egeMax | комментариев 37

Печать страницы

комментариев 37

← Предыдущие комментарии

Шукрулло

2017-04-30 в 15:59

Можете еще помочь с один уравнением:
log_4 x + log_2 x = 3
Думаю писал правильно.

[ Ответить ]
- egeMax
  
  2017-04-30 в 23:03
  
  $0,5log_2x+log_2x=3;$
  $1,5log_2x=3;$
  $log_2x=2;$
  $x=4.$
  
  [ Ответить ]
  - Шукрулло
    
    2017-05-01 в 10:02
    
    Я одно не понял. Как у Вас получилась 1,5log_2 x = 3 ? Какую формулу вы использывали? Искал, не нашол.
    
    [ Ответить ]
    - egeMax
      
      2017-05-01 в 20:10
      
      0,5+1=1,5
      
      [ Ответить ]
      - Шукрулло
        
        2017-05-01 в 20:25
        
        Лол) Понял. Спасибо большое
        
        [ Ответить ]

← Предыдущие комментарии

Добавить комментарий Отменить ответ

Найти:
Материалы для подготовки к ЕГЭ
№12 №14 №15 №17
Рубрики
- 01 Геометрия (12)
- 02 Стереометрия (9)
- 03 Теория вероятностей ч.1 (1)
- 04 Теория вероятностей ч.2 (1)
- 05 Простейшие уравнения (5)
- 06 Вычисления (5)
- 07 Производная, ПО (4)
- 08 «Прикладные» задачи (5)
- 09 Текстовые задачи (7)
- 10 Графики функций (7)
- 11 Исследование функции (2)
- 12 (С1) Уравнения (79)
- 13 (С2) Стереометр. задачи (95)
- 14 (С3) Неравенства (90)
- 15 (С4) Практич. задачи (72)
- 16 (С5) Планиметр. задачи (87)
- 17 (С6) Параметры* (80)
- 18 (С7) Числа, их свойства (39)
- A1 Простейшие текст/задачи (нет в ЕГЭ-22) (3)
- A2 Читаем графики (нет в ЕГЭ-22) (1)
- Видеоуроки (44)
- ГИА (11)
  - II часть (11)
- ЕГЭ (диагностич. работы) (70)
- Задачи (28)
- Иррациональные выражения, уравнения и неравенства (15)
- Логарифмы (39)
- МГУ (12)
- Метод интервалов (4)
- Метод рационализации (18)
- Модуль (9)
- Параметр (40)
- Переменка (5)
- Планиметрия (59)
- Показательные выражения, уравнения и неравенства (8)
- Разложение на множители (1)
- Рациональные выражения, уравнения и неравенства (10)
- Справочные материалы (92)
- Стереометрия (52)
- Т/P A. Ларина (443)
- Текстовые задачи (12)
- Теория чисел (2)
- Тесты по темам (80)
- Тригонометрические выражения, уравнения и неравенства (43)
- Функции и графики (10)
Дружественные сайты
Сайт А. Ларина ЕгэТренер – О. Себедаш Математика?Легко! Егэ? Ок! – И. Фельдман
Свежие записи
Архивы Архивы