Задание №18. Досрочный ЕГЭ 2018

Смотрите также задания №1-12; №13; №14; №15; №16; №17; №19

17. Найдите все значения параметра a, при каждом из которых система
уравнений

$\begin{cases}
((x+5)^2+y^2-a^2)\cdot ln(9-x^2-y^2)=0,\\
((x+5)^2+y^2-a^2)\cdot (x+y-a+5)=0;
\end{cases}$

имеет ровно два различных решения.

Решение:

$\\$
$\begin{cases}\left [ \begin{array}{rcl}(x+5)^2+y^2=a^2,\\ln(9-x^2-y^2)=0;\\ \end{array}\right.\\\left [ \begin{array}{rcl}(x+5)^2+y^2=a^2,\\x+y-a+5=0;\\ \end{array}\right.\\9-x^2-y^2>0;\end{cases}$

$\\$

$\left [ \begin{array}{rcl}\begin{cases}(x+5)^2+y^2=a^2,\\9-x^2-y^2>0;\\ \end{cases}\\\begin{cases}ln(9-x^2-y^2)=0,\\x+y-a+5=0;\end{cases}\end{array}\right.$

$\\$

$\left [ \begin{array}{rcl}\begin{cases}(x+5)^2+y^2=a^2,\\x^2+y^2<9;\\ \end{cases}\\\begin{cases}x^2+y^2=8,\\x+y-a+5=0;\end{cases}\end{array}\right.$
$\\$

$(x+5)^2+y^2=a^2$ – семейство окружностей с центром  $(-5;0),$ радиусом $|a|.$

$x^2+y^2<9$ – круг с открытой границей с центром $(0;0),$ радиусом $3$.

Первая система (*) указанной выше совокупности либо не имеет решений ($|a|\leq 2,$  $|a|\geq 8$), либо имеет бесконечно много решений ($2<|a|<8$). Поэтому, если мы хотим, чтобы исходная система имела бы два решения, необходимо, как минимум, потребовать, чтобы первая система (*) последней совокупности не имела бы решений. Также необходимо, чтобы вторая система (**) совокупности имела бы два решения.

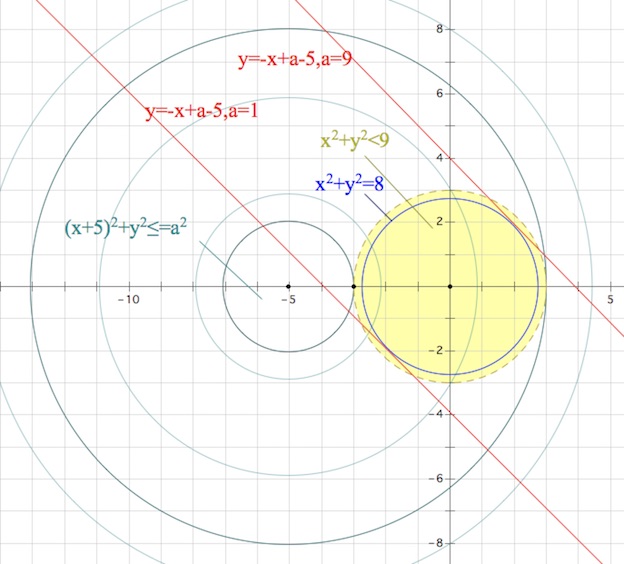
Первое требование, как мы уже замечали, выполняется при  $|a|\leq 2$ или $|a|\geq 8,$ то есть $a\in (-\infty;-8]\cup [-2;2]\cup [8;+\infty).$

Второе требование (система (**) имеет два решения) выполняется при $1<a<9.$
Действительно, прямая $y=-x-a+5$ должна занимать положение между параллельными прямыми $y=-x+4,$ $y=-x-4,$ ведь именно они отвечают за касание $x^2+y^2=8$ и $y=-x-a+5$  (если радиус окружности $2\sqrt2$ – высота равнобедренного прямоугольника треугольника, проведенная к гипотенузе, то катеты  равны $4$).

Итак,

$a\in (1;2]\cup [8;9).$

Ответ: $(1;2]\cup [8;9).$