Главная › 16 (С5) Планиметр. задачи › Задание №18 (С4) из Т/Р №87 А. Ларина

16 Окт 2014

Категория: 16 (С5) Планиметр. задачиПланиметрияТ/P A. Ларина

Задание №18 (С4) из Т/Р №87 А. Ларина

Елена Репина 2014-10-16 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №16»

Смотрите также задания №16, №17, №20.

Хорда $AB$ стягивает дугу окружности, равную 120°. Точка $C$ лежит на этой дуге, а точка $D$ лежит на хорде $AB$ . При этом $AD = 2,$ $BD = 1,$ $DC = \sqrt2$ .
а) Докажите, что угол $ADC$ равен $\frac{\pi}{6}.$
б) Найдите площадь треугольника $ABC$ .

Решение:

а) Замечаем: треугольник $AOB$ ( $O$ –центр окружности) – равнобедренный

( $AO=BO$ как радиусы), $\angle O=120^{\circ}$ , $AB=3$ .

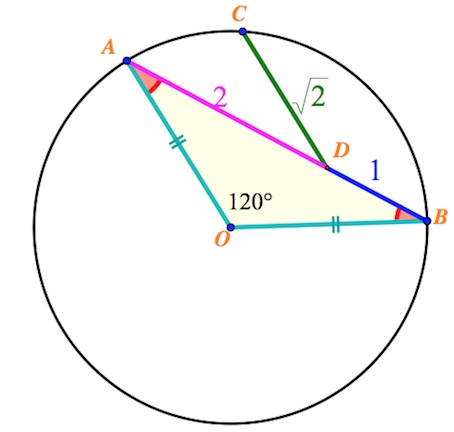
Тогда по т. косинусов:

$3^2=2AO^2-2AO^2\cdot cos120^{\circ};$

$9=3AO^2;$

$AO=\sqrt3.$

Применим и к треугольнику $ADO$ теорему косинусов:

$OD^2=AO^2+AD^2-2AO\cdot AD\cdot cos 30^{\circ};$

$OD^2=3+4-2\cdot \sqrt3\cdot 2\cdot \frac{\sqrt3}{2};$

$OD=1.$

Но тогда замечаем, что треугольник $ODC$ – прямоугольный, ведь

$OC=OA=\sqrt3$ , $CD=\sqrt2$ , $OD=1$ дают $OD^2+CD^2=OC^2$ .

Далее внешний угол $ADO$ равнобедренного треугольника $ODB$ , есть сумма углов $DOB$ и $DBO$ , то есть $\angle ADO=60^{\circ}.$

Наконец,

$\angle ADC=\angle ODC-\angle ODA=90^{\circ}-60^{\circ}=30^{\circ}.$

Что и требовалось доказать.

б) Найдем площадь треугольника $ABC:$

$S_{ABC}=S_{ACD}+S_{CDB};$

$S_{ABC}=\frac{1}{2}\cdot AD\cdot CD\cdot sinADC+\frac{1}{2}\cdot CD\cdot DB\cdot sinCDB;$

$S_{ABC}=\frac{1}{2}(2\cdot \sqrt2\cdot \frac{1}{2}+\sqrt2\cdot 1\cdot \frac{1}{2});$

$S_{ABC}=\frac{3\sqrt2}{4}.$

Ответ: $\frac{3\sqrt2}{4}.$

Автор: egeMax | комментариев 6

Печать страницы

комментариев 6

Алена

2014-10-16 в 20:42

Как здорово, что я встретила ваш сайт. красивые решения. красивые рисунки. спасибо. буду у вас учиться Елена Юрьевна.

[ Ответить ]
- egeMax
  
  2014-10-16 в 20:43
  
  Алена, добро пожаловать! ;)
  
  [ Ответить ]
Ольга

2015-03-20 в 19:37

Здравствуйте, а почему CD=корень из 2, если DC=2?

[ Ответить ]
- egeMax
  
  2015-03-20 в 19:53
  
  Ольга, в самом условии не пропечатался корень… СD=корень из 2.
  Подправила. Спасибо!
  
  [ Ответить ]
Ольга

2015-04-03 в 21:50

Спасибо вам за хорошие решения. Узнаю много нового для себя.

[ Ответить ]
- egeMax
  
  2015-04-04 в 07:11
  
  ;)
  
  [ Ответить ]

Добавить комментарий Отменить ответ

Найти:
Материалы для подготовки к ЕГЭ
№12 №14 №15 №17
Рубрики
- 01 Геометрия (12)
- 02 Стереометрия (9)
- 03 Теория вероятностей ч.1 (1)
- 04 Теория вероятностей ч.2 (1)
- 05 Простейшие уравнения (5)
- 06 Вычисления (5)
- 07 Производная, ПО (4)
- 08 «Прикладные» задачи (5)
- 09 Текстовые задачи (7)
- 10 Графики функций (7)
- 11 Исследование функции (2)
- 12 (С1) Уравнения (79)
- 13 (С2) Стереометр. задачи (95)
- 14 (С3) Неравенства (90)
- 15 (С4) Практич. задачи (72)
- 16 (С5) Планиметр. задачи (87)
- 17 (С6) Параметры* (80)
- 18 (С7) Числа, их свойства (39)
- A1 Простейшие текст/задачи (нет в ЕГЭ-22) (3)
- A2 Читаем графики (нет в ЕГЭ-22) (1)
- Видеоуроки (44)
- ГИА (11)
  - II часть (11)
- ЕГЭ (диагностич. работы) (70)
- Задачи (28)
- Иррациональные выражения, уравнения и неравенства (15)
- Логарифмы (39)
- МГУ (12)
- Метод интервалов (4)
- Метод рационализации (18)
- Модуль (9)
- Параметр (40)
- Переменка (5)
- Планиметрия (59)
- Показательные выражения, уравнения и неравенства (8)
- Разложение на множители (1)
- Рациональные выражения, уравнения и неравенства (10)
- Справочные материалы (92)
- Стереометрия (52)
- Т/P A. Ларина (443)
- Текстовые задачи (12)
- Теория чисел (2)
- Тесты по темам (80)
- Тригонометрические выражения, уравнения и неравенства (43)
- Функции и графики (10)
Дружественные сайты
Сайт А. Ларина ЕгэТренер – О. Себедаш Математика?Легко! Егэ? Ок! – И. Фельдман
Свежие записи
Архивы Архивы