Задание № 18 (С4) Т/Р №93 А. Ларина

Смотрите также №15, №16, №17, №19, №20

В трапеции $ABCD$ $BC$ и $AD$ – основания. Биссектриса угла $A$ пересекает сторону $CD$ в ее середине – точке $P$.
а) Докажите, что $BP$ – биссектриса угла $ABC$.
б) Найдите площадь трапеции $ABCD$, если известно, что $AP=8$, $BP=6$.

Решение:

a) Докажем, что $BP$ – биссектриса угла $B.$

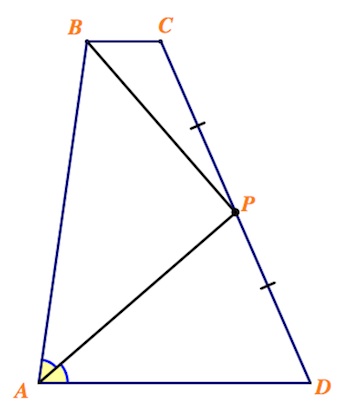
Пусть $N$ – середина $AB$. Тогда $NP$ – средняя линия трапеции, в частности, $NP||AD||BC.$

Углы $1$ и $3$ (см. рис.) – внутренние накрест лежащие углы при параллельных прямых $AD, NP$ и секущей $AP$, значит $\angle 1=\angle 3$.

С учетом условия $\angle 1=\angle 2$, получаем: $\angle 2=\angle 3$, то есть $\Delta ANP$ – равнобедренный.

Но тогда автоматически равнобедренным становится и треугольник $NPB$. То есть $\angle 4=\angle 5$. А поскольку $\angle 4=\angle 6$ (накрест лежащие при $BC||NP$ и секущей $BP$), то приходим к тому, что $\angle 5=\angle 6$, то есть $BP$ – биссектриса угла $B.$

б) Так как точка $N$ равноудалена от точек $A,B$ и $P$, то $N$ – центр окружности, описанной около треугольника $ABP$. А поскольку сторона $AB$ – диаметр этой окружности, то угол $APB$ – прямой.

Пусть лучи $BC$ и $AP$ пересекаются в точке $F$.

Треугольники $CFP$ и $DAP$ равны по второму признаку.

Будем рассматривать площадь трапеции $S_{ABCD}$ как $S_{APB}+S_{BFP},$ то есть нам требуется найти площадь треугольника $ABF$.

При этом треугольники $ABP$ и $FBP$, из которых состоит треугольник $ABF$ равны по двум катетам.

$S_{ABCD}=2\cdot \frac{6\cdot 8}{2}=48.$

Ответ: 48.