Главная › 16 (С5) Планиметр. задачи › Задание №18 (С4) Т/Р №94 А. Ларина

04 Дек 2014

Категория: 16 (С5) Планиметр. задачиПланиметрияТ/P A. Ларина

Задание №18 (С4) Т/Р №94 А. Ларина

Елена Репина 2014-12-04 2016-09-07

В новом формате ЕГЭ по математике задание значится как «Задание №16»

Смотрите также №15 , №16, №17, №19, №20.

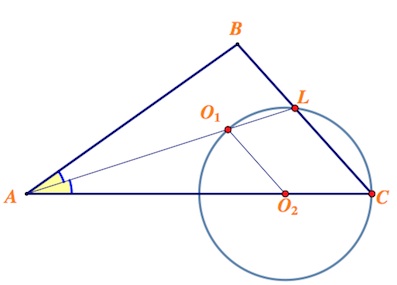
В треугольнике $ABC$ $AB=20$ , $AC=24$ . Окружность с центром $O_2$ на стороне $AC$ проходит через вершину $C$ , точку пересечения биссектрисы угла $A$ со стороной $BC$ и центр $O_1$ вписанной в треугольник $ABC$ окружности.
а) Докажите, что прямая $O_1O_2$ параллельна прямой $BC$ ;
б) Найдите радиус описанной около треугольника $ABC$ окружности.

Решение:

a) Докажем, что $O_1O_2||BC.$

лотло

Центр вписанной окружности в треугольник – точка пересечения его биссектрис. Обозначив угол $BCO_1$ за $\alpha$ , получаем, что и $\angle O_1CO_2=\alpha.$

Вписанный угол $O_1CA$ опирается на ту же дугу, что и центральный угол $O_1O_2A$ , поэтому $\angle O_1O_2A=2\alpha.$

Итак, $\angle BCA=\angle O_1O_2A$ , а поскольку углы – соответственные при прямых $BC$ , $O_1O_2$ и секущей $O_1C$ , то $O_1O_2||BC$ по признаку параллельности прямых.

б) Пусть биссектриса угла $A$ пересекает сторону $BC$ в точке $L.$ Вписанный угол $O_1LC$ , опирающийся на дугу $O_1C$ (большую), равную $2\alpha+180^{\circ}$ , равен $\alpha +90^{\circ}.$ Угол $BLA$ , смежный с углом $ALC$ , есть $90^{\circ}-\alpha.$

ijh

Из треугольника $ALC$ :

$\angle LAC=180^{\circ}-(\angle C+\angle L)=90^{\circ}-3\alpha.$

Тогда и $\angle BAL=90^{\circ}-3\alpha$ .

Из треугольника $ABL$ : $\angle B=180^{\circ}-(\angle A+\angle L)=4\alpha.$

Распишем площадь треугольника $ABC$ двумя способами:

$S=\frac{AB\cdot BC\cdot sin 4\alpha}{2};$

$S=\frac{AC\cdot BC\cdot sin 2\alpha}{2};$

Откуда

$20sin4\alpha=24sin2\alpha$

или

$40sin2\alpha cos2\alpha=24sin2\alpha;$

$cos2\alpha=\frac{3}{5}.$

Заметим, $sin2\alpha=\sqrt{1-(\frac{3}{5})^2}=\frac{4}{5}.$

Применим теорему синусов к треугольнику $ABC:$

$\frac{AC}{sinB}=2R$ ,

где $R$ – радиус окружности, описанной около треугольника $ABC$ .

$\frac{24}{sin4\alpha}=2R;$

$R=\frac{12}{2sin2\alpha cos2\alpha}=\frac{12}{2\cdot \frac{4}{5}\cdot \frac{3}{5}}=12,5.$

Ответ: 12,5.

Автор: egeMax | комментария 2

Печать страницы

комментария 2

Дима

2015-03-25 в 13:04

Почему угол L=90+a?

[ Ответить ]
- egeMax
  
  2015-03-25 в 14:19
  
  Потому что он вписанный, опирается на дугу 180+2a
  
  [ Ответить ]

Задание №18 (С4) Т/Р №94 А. Ларина

Добавить комментарий Отменить ответ