Задание №18 (С4) Т/Р №96 А. Ларина

Смотрите также №15,  №16, №17, №19, №20.

В окружность вписан четырехугольник $ABCD$, диагонали которого перпендикулярны и пересекаются в точке $E$. Прямая, проходящая через точку $E$ и перпендикулярная к $AB$, пересекает сторону $CD$ в точке $M$.

а) Докажите, что $EM$ – медиана треугольника $CED$.
б) Найдите длину отрезка $EM$, если $AD=8$, $AB=4$ и угол $CDB$ равен $60^{\circ}$.

Решение:

a) $\angle BAC=\angle BDC$ (вписанные углы, опирающиеся на одну дугу).

$\angle MED$ и  $\angle FAE$ дополняют равные углы $CEM$ и $FEA$ соответственно  до $90^{\circ}$, а значит они равны между собой.

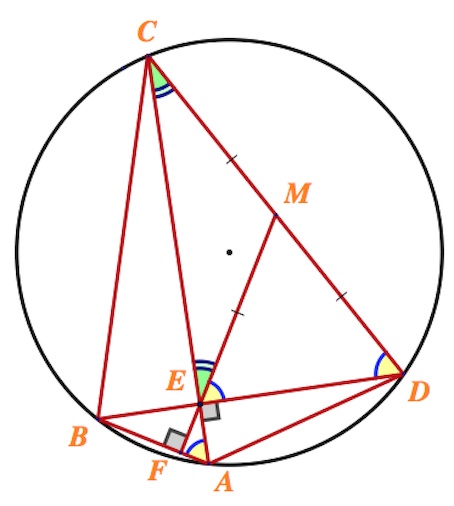
Далее, углы $CEM$ и $ECD$ дополняют равные углы $MED$ и $EDC$ соответственно до $90^{\circ}$, а значит оказываются равными.

Итак, треугольники $EMD$ и $EMC$ оказываются равнобедренными (с основаниями $ED$ и $CE$ соответственно). Значит $EM=MD=MC$ и, в частности,  $EM$ – медиана треугольника $CED$.

б) $\Delta BAE:$

$AB=4$,   $\angle BAE=60^{\circ}$. Имеем:  $AE=\frac{AB}{2}=2.$

$\Delta AED:$

$ED=\sqrt{AD^2-AE^2}=\sqrt{8^2-2^2}=2\sqrt{15}.$

Треугольник $EMD$ – равносторонний. $EM=ED=2\sqrt{15}.$

Ответ: $2\sqrt{15}.$