Задание №18 (С4) Т/Р №97 А. Ларина

Две окружности касаются внешним образом в точке $A$. Прямая $l$ касается первой окружности в точке $B$, а второй – в точке $C$.
a) Докажите, что треугольник $ABC$ прямоугольный.
б) Найдите площадь треугольника $ABC$, если радиусы окружностей 8 и 2.

Решение:

a) Проведем общую касательную к окружностям через точку $A$. Пусть она пересекает прямую $l$ в точке $A$.

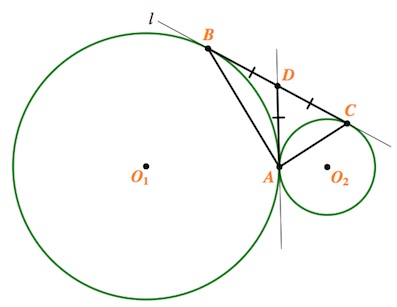
По свойству отрезков касательных имеем: $AD=BD$ и $AD=DC$, то есть точка $D$ равноудалена от всех вершин треугольника $ABC$.

Итак, точка $D$ – центр описанной окружности около треугольника $ABC$, при этом $BC$ – диаметр этой окружности.  Угол $A$, опирающийся на диаметр, – прямой.

б) Пусть $O_1, O_2$ – центры большой и малой окружностей соответственно.

Заметим, $O_1B\perp l$ и $O_2C\perp l$.

Проведем через центр меньшей окружности  прямую, параллельную $l$. Пусть она пересекает $O_1B$ в точке $E$.

Треугольник $O_1EO_2$ – прямоугольный, известны его гипотенуза и один из катетов. Тогда $EO_2=BC=\sqrt{10^2-6^2}=8.$

Заметим, $sin ADB=sinADC$, так как $\angle ADB+\angle ADC=180^{\circ}$.

$S_{ABC}=S_{ABD}+S_{ADC}=\frac{1}{2}AD\cdot BD\cdot sinADB+\frac{1}{2}AD\cdot DC\cdot sinADC=$

$=(\frac{BC}{2})^2sinADB$.

Заметим, $sin ADB=sinO_1$, так как в четырехугольнике $AO_1BD$ на сумму углов $A$ и $B$, а значит и на сумму углов $O_1$ и $ADB$, приходится $180^{\circ}.$

Из треугольника $O_1EO_2:$    $sinO_1=\frac{8}{10}=\frac{4}{5}.$

Итак, $S_{ABC}=(\frac{BC}{2})^2sinO_1=16\cdot \frac{4}{5}=12,8.$

 Ответ: 12,8.