Главная › 16 (С5) Планиметр. задачи › Задание №18 Т/Р №101 А. Ларина

15 Янв 2015

Категория: 16 (С5) Планиметр. задачиПланиметрияТ/P A. Ларина

Задание №18 Т/Р №101 А. Ларина

Елена Репина 2015-01-15 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №16»

Смотрите также №15, №16, №17, №19, №20.

В остроугольном треугольнике $ABC$ высоты $AA_1$ и $CC_1$ пересекаются в точке $O$ .

а) Докажите, что треугольники $AOC$ и $C_1OA_1$ подобны.

б) Найдите площадь четырехугольника $ACA_1C_1$ , если известно, что угол $ABC$ равен $30^{\circ}$ , а площадь треугольника $ABC$ равна $80^{\circ}$ .

Решение:

а) Точки $A, C, A_1, C_1$ лежат на одной окружности с диаметром $AC.$

kjh

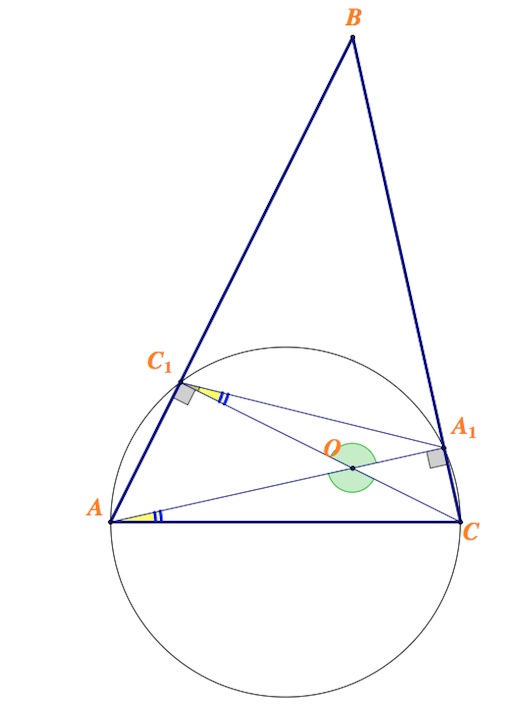
Поэтому $\angle A_1AC=\angle A_1C_1C$ как вписанные углы, опирающиеся на одну дугу.

Заметим, $\angle AOC=\angle A_1OC_1$ как вертикальные.

Тогда $\Delta AOC\infty \Delta A_1OC_1$ по двум углам.

б) Так по условию $\angle B=30^{\circ}$ и $S_{ABC}=80$ , то

$80=\frac{1}{2}\cdot AB\cdot BC\cdot sin 30^{\circ};$

$320=AB\cdot BC;$

Из прямоугольного треугольника $AA_1B$ с углом в $30^{\circ}$ $AA_1=\frac{AB}{2}.$

Аналогично $CC_1=\frac{BC}{2}.$

Распишем площадь четырехугольника $ACA_1C_1:$

$S_{ACA_1C_1}=\frac{1}{2}\cdot AA_1\cdot CC_1\cdot sin O;$

$S_{ACA_1C_1}=\frac{1}{2}\cdot \frac{AB}{2}\cdot \frac{BC}{2}\cdot sin 150^{\circ};$

$S_{ACA_1C_1}=\frac{1}{16}\cdot AB\cdot BC;$

$S_{ACA_1C_1}=20.$

Ответ: 20.

Автор: egeMax | комментариев 10

Печать страницы

комментариев 10

Искандер

2015-05-10 в 14:38

Достаточно ли для доказательства пункта а) указать, что треугольники АС1О и А1СО подобны (по двум углам) (отсюда следует что OC1/OA1=OA/OC), а углы С1ОА1 и АОС равны как вертикальные?

[ Ответить ]
- egeMax
  
  2015-05-10 в 15:46
  
  Да, конечно.
  
  [ Ответить ]
  - Роман
    
    2015-05-21 в 23:37
    
    Почему?
    
    [ Ответить ]
  - Роман
    
    2015-05-21 в 23:45
    
    Почему мы может так это утверждать?
    
    [ Ответить ]
    - egeMax
      
      2015-05-22 в 10:23
      
      Роман, поконкретней можно? В чем вопрос?
      
      [ Ответить ]
      - Роман
        
        2015-05-22 в 10:56
        
        Почему за счет подобия одних треугольников можно доказать подобие других?
        
        [ Ответить ]
      - egeMax
        
        2015-05-22 в 11:00
        
        Первая пара треугольников подобна по двум углам (I признак). Из подобие этой пары треугольников в свою очередь следует пропорциональность соответствующих сторон. А также замечаем, что углы, о которых говорил Искандер, равны.
        То есть вторая пара треугольников уже подобна по двум пропорциональным сторонам и углу между ними (II признак).
        
        [ Ответить ]
Роман

2015-05-22 в 18:20

Тогда поконкретней)Почему около четырехугольника AC1A1C можно описать окружность?нам ведь не известно что сумма противоположных углов равна 180?
Второй вопрос:из подобия прямоугольрых треугольников следует ,что сторона AO подобна ОС,а на надо доказать что AO ПОДОБНА OC1?заранее спасибо)

[ Ответить ]
- egeMax
  
  2015-05-22 в 19:07
  
  1) Раз треугольники $ACC_1,AA_1C$ имеют общую гипотенузу, то они оказываются вписанными в одну окружность. Посудите сами. Около треугольника всегда можно описать окружность, так? То есть около одного их треугольников, например, около $ACC_1$ она уже описана. Остается только выяснить, попадет ли четвертая точка, точка $A_1$ на эту окружность. Как вы думаете, попадет?
  2) Из подобия треугольников $AOC_1,COA_1$ следует не подобие, а пропорциональность соответствующих сторон $AO,CO$ и $OC_1,OA_1$ .
  
  [ Ответить ]
  - Роман
    
    2015-05-22 в 23:37
    
    Благодарю за подробное пояснение!
    
    [ Ответить ]

Добавить комментарий Отменить ответ

Найти:
Материалы для подготовки к ЕГЭ
№12 №14 №15 №17
Рубрики
- 01 Геометрия (12)
- 02 Стереометрия (9)
- 03 Теория вероятностей ч.1 (1)
- 04 Теория вероятностей ч.2 (1)
- 05 Простейшие уравнения (5)
- 06 Вычисления (5)
- 07 Производная, ПО (4)
- 08 «Прикладные» задачи (5)
- 09 Текстовые задачи (7)
- 10 Графики функций (7)
- 11 Исследование функции (2)
- 12 (С1) Уравнения (79)
- 13 (С2) Стереометр. задачи (95)
- 14 (С3) Неравенства (90)
- 15 (С4) Практич. задачи (72)
- 16 (С5) Планиметр. задачи (87)
- 17 (С6) Параметры* (80)
- 18 (С7) Числа, их свойства (39)
- A1 Простейшие текст/задачи (нет в ЕГЭ-22) (3)
- A2 Читаем графики (нет в ЕГЭ-22) (1)
- Видеоуроки (44)
- ГИА (11)
  - II часть (11)
- ЕГЭ (диагностич. работы) (70)
- Задачи (28)
- Иррациональные выражения, уравнения и неравенства (15)
- Логарифмы (39)
- МГУ (12)
- Метод интервалов (4)
- Метод рационализации (18)
- Модуль (9)
- Параметр (40)
- Переменка (5)
- Планиметрия (59)
- Показательные выражения, уравнения и неравенства (8)
- Разложение на множители (1)
- Рациональные выражения, уравнения и неравенства (10)
- Справочные материалы (92)
- Стереометрия (52)
- Т/P A. Ларина (443)
- Текстовые задачи (12)
- Теория чисел (2)
- Тесты по темам (80)
- Тригонометрические выражения, уравнения и неравенства (43)
- Функции и графики (10)
Дружественные сайты
Сайт А. Ларина ЕгэТренер – О. Себедаш Математика?Легко! Егэ? Ок! – И. Фельдман
Свежие записи
Архивы Архивы