Главная › 16 (С5) Планиметр. задачи › Задание №18 Т/Р №104 А. Ларина

12 Фев 2015

Категория: 16 (С5) Планиметр. задачиПланиметрияТ/P A. Ларина

Задание №18 Т/Р №104 А. Ларина

Елена Репина 2015-02-12 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №16»

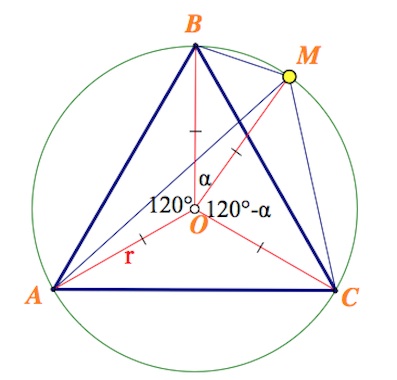
Равносторонний треугольник $ABC$ вписан в окружность. На окружности отмечена точка $M$ , не совпадающая ни с одной из точек $A$ , $B$ и $C$ .

а) Докажите, что расстояние от точки $M$ до одной из вершин треугольника равно сумме расстояний до двух других вершин.

б) Найдите периметр четырехугольника с вершинами в точках $A$ , $B$ , $C$ и $M$ , если известно, что его площадь равна $\frac{49\sqrt3}{4}$ , а радиус окружности равен $\sqrt{13}$ .

Решение:

а) Пусть $M$ – между $B$ и $C.$ Докажем, что $AM=BM+CM.$

В остальных случаях рассуждения аналогичные.

Пусть $\alpha=\angle BOM,$ $r$ – радиус окружности, описанной около $\Delta ABC$ .

Из треугольника $OBM$ ( $O$ – центр $\Delta ABC$ ) по т. Косинусов:

$BM^2=r^2+r^2-2r^2cos\alpha.$

Из треугольника $OMC$ по т. Косинусов:

$MC^2=r^2+r^2-2r^2cos(120^{\circ}-\alpha).$

Из треугольника $OAM$ по т. Косинусов:

$AM^2=r^2+r^2-2r^2cos(120^{\circ}+\alpha).$

Тогда

$BM+CM-AM=\sqrt2r(\sqrt{1-cos\alpha}+\sqrt{1-cos(120^{\circ}-\alpha)}-\sqrt{1-cos(120^{\circ}+\alpha)})=$

$=\sqrt2r(\sqrt{2sin^2\frac{\alpha}{2}}+\sqrt{2sin^2(60^{\circ}-\frac{\alpha}{2})}-\sqrt{2sin^2(60^{\circ}+\frac{\alpha}{2})})=$

$=2r(|sin\frac{\alpha}{2}|+|sin(60^{\circ}-\frac{\alpha}{2})|-|sin(60^{\circ}+\frac{\alpha}{2})}|)=$

$=2r(sin\frac{\alpha}{2}+sin(60^{\circ}-\frac{\alpha}{2})-sin(60^{\circ}+\frac{\alpha}{2})})=$

$=2r(sin\frac{\alpha}{2}+\frac{\sqrt3}{2}cos\frac{\alpha}{2}-\frac{1}{2}sin\frac{\alpha}{2}-\frac{\sqrt3}{2}cos\frac{\alpha}{2}-\frac{1}{2}sin\frac{\alpha}{2})=0,$

то есть $BM+CM=AM$ .

Что и требовалось доказать.

б) Поскольку радиус окружности, описанной около $\Delta ABC$ равен $\sqrt{13}$ , то сторона $a$ треугольника $ABC$ есть $\sqrt{39}.$

Заметим, $\angle BFM=\frac{1}{2}(\alpha + 120^{\circ})$ $(F$ – точка пересечения $BC$ и $AM).$

Имеем

$S_{ABMC}=\frac{1}{2}BC\cdot AMsin\angle BFM;$

$\frac{49\sqrt3}{4}=\frac{1}{2}\sqrt{39}AMsin(\frac{\alpha}{2}+60^{\circ})$ (*)

При этом $AM=\sqrt2r\sqrt{1-cos(\alpha+120^{\circ})}= 2\sqrt{13}sin(\frac{\alpha}{2}+60^{\circ}).$

Тогда $sin(\frac{\alpha}{2}+60^{\circ})=\frac{AM}{2\sqrt{13}}.$ Подставляем в (*):

$\frac{49\sqrt3}{4}=\frac{1}{2}\sqrt{39}\frac{AM^2}{2\sqrt{13}};$

$AM=7.$

Наконец,

$P_{ABMC}=2\sqrt{39}+BM+MC=2\sqrt{39}+AM=2\sqrt{39}+7.$

Ответ: $2\sqrt{39}+7.$

Автор: egeMax | комментария 3

Печать страницы

комментария 3

Дима

2015-03-15 в 14:56

Почему угол BFM=(120°+a)/2? Можно подробней?

[ Ответить ]
- egeMax
  
  2015-03-15 в 16:23
  
  Дмитрий, есть такое свойство:
  Угол между двумя пересекающимися хордами равен полусумме высекаемых ими дуг.
  Попробуйте доказать – хороше свойство.
  Если не получится – обращайтесь, будем вместе разбираться… ;)
  
  [ Ответить ]
Дима

2015-03-15 в 18:55

Большое спасибо, совсем забыл про это свойство:)

[ Ответить ]

Задание №18 Т/Р №104 А. Ларина

Добавить комментарий Отменить ответ