Задание №18 Т/Р №105 А. Ларина

Смотрите также №15, №16, №17, №19, №20

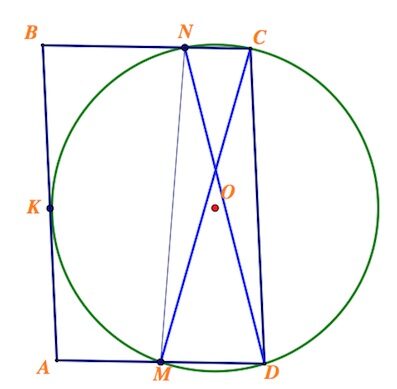
Окружность касается стороны $AB$ параллелограмма $ABCD$, пересекает стороны $AD$ и $BC$ в точках $M$ и $N$ соответственно и проходит через вершины $C$ и $D$.
а) Докажите, что $DN=CM$.
б) Найдите $DN$, зная, что $AM=9$, $BN=16$, $ВС=18.$

Решение:

a) Четырехугольник $NCDM$, вписанный в окружность, – трапеция.  А раз трапеция вписана в окружность, то она равнобедренная.

Тогда диагонали $CM$ и $DN$ равны.

Что и требовалось доказать.

б) По свойству касательной и секущей, проведенных из одной точки к окружности $BK^2=BN\cdot BC$, то есть $BK^2=16\cdot 18$, откуда $BK=12\sqrt2.$

Аналогично $AK^2=AM\cdot AD$, откуда $AK=9\sqrt2.$

Пусть $NH_1\perp AD$ и $CH_2\perp AD$.

Имеем: $MH_1=DH_2=\frac{9-2}{2}=\frac{7}{2}.$

Из прямоугольного треугольника $CDH_2:$

$CH_2^2=CD^2-H_2D^2=(21\sqrt2)^2-(\frac{7}{2})^2=\frac{3528-49}{4}=\frac{3479}{4}.$

Из прямоугольного треугольника $MCH_2$:

$MC=\sqrt{MH_2^2+CH_2^2}=\sqrt{(\frac{11}{2})^2+\frac{3479}{4}}=\sqrt{\frac{3600}{4}}=30.$

Ответ: 30.