Главная › 16 (С5) Планиметр. задачи › Задание №18 Т/Р №106 А. Ларина

26 Фев 2015

Категория: 16 (С5) Планиметр. задачиПланиметрияТ/P A. Ларина

Задание №18 Т/Р №106 А. Ларина

Елена Репина 2015-02-26 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №16»

Смотрите также №15, №16, №17, №19, №20.

В равнобедренном треугольнике $ABC$ ( $AB=BC$ ) проведены высоты $AK$ , $BM$ и $CP$ .

a) Докажите, что треугольник $KMP$ – равнобедренный.

б) Найдите площадь треугольника $ABC$ , если известно, что площадь треугольника $KMP$ равна 12, а косинус угла $ABC$ равен 0,6.

Решение:

а)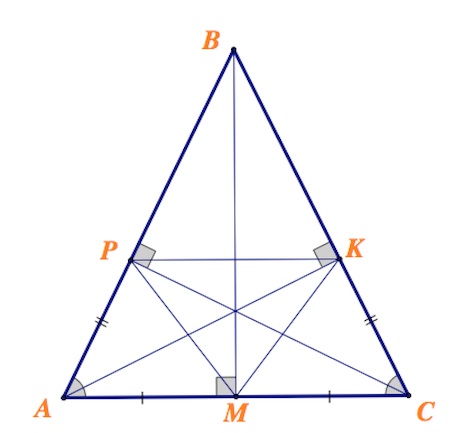

Треугольники $AKC$ и $CPA$ равны по гипотенузе и острому углу ( $AC$ – общая, $\angle A=\angle C$ (углы при основании равнобедренного треугольника)). Тогда $CK=AP.$

Треугольники $APM$ и $CKM$ равны по двум сторонам и углу между ними ( $AM=CM, AP=CK, \angle A=\angle C$ ), откуда следует, что $PM=KM,$ то есть треугольник $KMP$ – равнобедренный.

Что и требовалось доказать.

б) Из треугольника $BPC:$

$cosABC=0,6=\frac{PB}{BC}.$

Пусть тогда $PB=6x, BC=10x.$ Очевидно, $AP=CK=4x.$

Опять же, из треугольника $BPC:$

$PC=\sqrt{(10x)^2-(6x)^2}=8x.$

Из треугольника $APC:$

$AC=\sqrt{(4x)^2+(8x)^2}=4\sqrt5x.$

oik

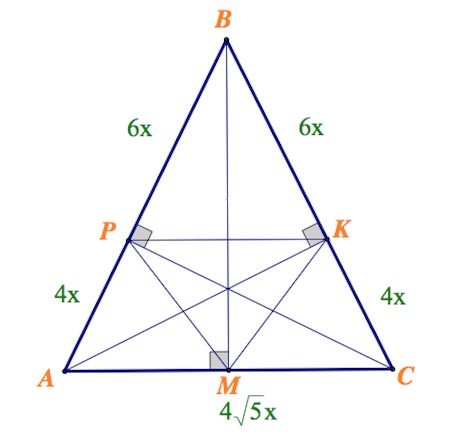
Заметим, $sinB=0,8$ (из $\Delta BPC$ ) и $sinA=\frac{2}{\sqrt5}$ (из $\Delta APC$ ).

Далее $S_{ABC}=2S_{APM}+12+S_{PBK}.$

Тогда

$\frac{AB^2\cdot sinB}{2}=2\cdot \frac{AP\cdot AM\cdot sinA}{2}+12+\frac{PB^2\cdot sinB}{2};$

$\frac{(10x)^2\cdot 0,8}{2}=2\cdot \frac{4x\cdot 2\sqrt5x\cdot \frac{2}{\sqrt5}}{2}+12+\frac{(6x)^2\cdot 0,8}{2};$

$40x^2=16x^2+12+\frac{72x^2}{5};$

$48x^2=12\cdot 5;$

$x^2=\frac{5}{4}.$

Наконец,

$S_{ABC}=\frac{(10x)^2\cdot 0,8}{2}=\frac{100\cdot \frac{5}{4}\cdot 0,8}{2}=\frac{100\cdot 5\cdot 4}{2\cdot 4\cdot 5}=50.$

Ответ: 50.

Вы можете найти аналогичную задачу здесь.

Автор: egeMax | комментария 3

Печать страницы

комментария 3

Татьяна Евгеньевна Бондаренко

2015-04-02 в 20:27

Уважаемая Елена Юрьевна, хотелось бы предложить ещё один способ вычисления площади S треугольника АВС. Если учесть, что ему подобен треугольник КВР с коэффициентом 0,6,то площадь треугольника КВР=0,36S.
Площадь треугольника МРК относится к сумме площадей треугольников АРМ и МКС как РК к АС,то есть отношение равно 0,6. Так как площадь треугольника МРК равна 12, то сумма площадей указанных треугольников 12:0,6=20. Таким образом, O,36S+12+20=S. Откуда S=50. Ещё раз спасибо за внимание.

[ Ответить ]
- egeMax
  
  2015-04-02 в 21:08
  
  Татьяна Евгеньевна, спасибо! Ни убавить, ни прибавить – стройно, красиво!
  
  [ Ответить ]
Татьяна Евгеньевна Бондаренко

2015-04-02 в 21:12

Спасибо, мне радостно.

[ Ответить ]

Задание №18 Т/Р №106 А. Ларина

Добавить комментарий Отменить ответ