Задание №18 Т/Р №204 А. Ларина

Смотрите также №13; №14; №15; №16; №17; №19 Тренировочной работы №204 А. Ларина.

18. Найти все $a$, при каждом из которых система

 $\begin{cases}
y-ax=a+5,\\
xy^2-x^2y-2xy+4x-4y+8=0;&
\end{cases}$

имеет ровно два решения.

Решение:

 $\begin{cases}
y=a(x+1)+5,\\
xy(y-x-2)-4(y-x-2)=0;&
\end{cases}$

$\begin{cases}
y=a(x+1)+5,\\
(xy-4)(y-x-2)=0;&
\end{cases}$

$\begin{cases}y=a(x+1)+5,\\\left[\begin{array}{rcl}y=\frac{4}{x},\\y=x+2;\end{array}\right.&\end{cases}$

$\begin{cases}y=a(x+1)+5,\\\left[\begin{array}{rcl}y=\frac{4}{x},\\y=x+2;\end{array}\right.&\end{cases}$

График первой строки исходной системы – семейство прямых, проходящих через точку $(-1;5).$

График второй строки исходной системы – объединение гиперболы $y=\frac{4}{x}$ и прямой $y=x+2.$

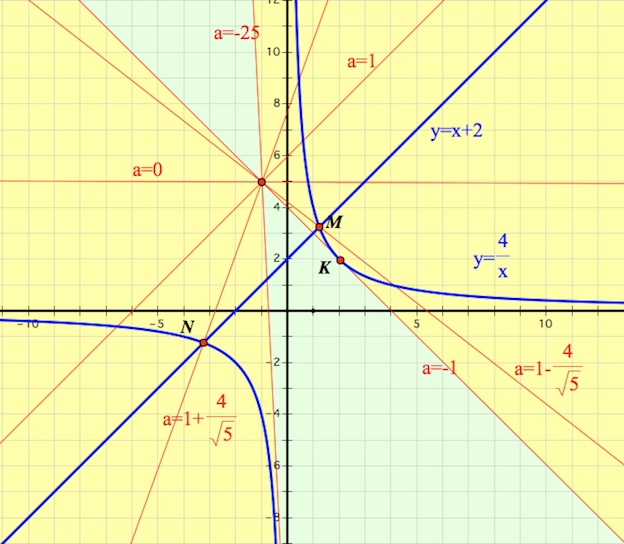
1) Найдем $a$,  отвечающее за прохождение прямой $y=a(x+1)+5$ через точку пересечения $y=\frac{4}{x}$, $y=x+2.$

Решив систему уравнений

$\begin{cases}y=\frac{4}{x},\\y=x+2,&\end{cases}$

получим координаты точек пересечения $y=\frac{4}{x}$, $y=x+2:$

$N (-1-\sqrt5;1-\sqrt5),$  $M(-1+\sqrt5;1+\sqrt5)$.

Откуда,  $a=1+\frac{4}{\sqrt5}$ (соответствует прохождению прямой $y=a(x+1)+5$  через точку $N$) или $a=1-\frac{4}{\sqrt5}$ (соответствует прохождению прямой $y=a(x+1)+5$  через точку $M$).

2) В случае, когда прямая $y=a(x+1)+5$ параллельна прямой $y=x+2,$ то есть при $a=1$, мы имеем две точки пересечения прямой $y=a(x+1)+5$ и множества точек $(xy-4)(y-x-2)=0.$

3) В случае, когда прямая $y=a(x+1)+5$ параллельна оси $(ox),$ то есть при $a=0$, мы имеем две точки пересечения прямой $y=a(x+1)+5$ и множества точек $(xy-4)(y-x-2)=0.$

4) Найдем $a,$ отвечающее за касание прямой $y=a(x+1)+5$ и гиперболы $y=\frac{4}{x}.$

Так как уравнение касательной к гиперболе $y=\frac{4}{x}$, проведенной через точку $(x_0;y(x_0))$ имеет вид  $y=-\frac{4}{x_0^2}(x-x_0)+\frac{4}{x_0},$ то составим систему:

$\begin{cases}-\frac{4}{x_0^2}=a,\\\frac{4}{x_0}+\frac{4}{x_0}=a+5,&\end{cases}$

$\begin{cases}-\frac{4}{x_0^2}=a,\\-\frac{4}{x_0}+\frac{4}{x_0}=-\frac{4}{x_0^2}+5;&\end{cases}$

$\begin{cases}-\frac{4}{x_0^2}=a,\\(\frac{2}{x_0})^2+4\cdot \frac{2}{x_0}-5=0;&\end{cases}$

$\begin{cases}-\frac{4}{x_0^2}=a,\\(\frac{2}{x_0})^2+4\cdot \frac{2}{x_0}-5=0;&\end{cases}$

$\begin{cases}-\frac{4}{x_0^2}=a,\\\left[\begin{array}{rcl}\frac{2}{x_0}=-5,\\\frac{2}{x_0}=1;\end{array}\right.&\end{cases}$

$\begin{cases}-\frac{4}{x_0^2}=a,\\\left[\begin{array}{rcl}x_0=-0,4,\\x_0=2;\end{array}\right.&\end{cases}$

Откуда $a=-1$ или $a=-25$.

На рисунке красными линиями  помечены те положения прямой $y=a(x+1)+5,$ которые будут давать ровно два пересечения с множеством точек $(xy-4)(y-x-2)=0.$

Салатовым цветом указана зона расположения прямых $y=a(x+1)+5,$ отвечающих за одно решение исходной системы.

Желтым цветом указана зона расположения прямых $y=a(x+1)+5,$ отвечающих за три решения исходной системы.

Итак, укажем $a,$ при которых исходная система будет давать два решения:

${-25;\pm 1;0;1\pm \frac{4}{\sqrt5}}.$

Ответ: ${-25;\pm 1;0;1\pm \frac{4}{\sqrt5}}.$