Главная › 17 (С6) Параметры* › Задание №18 Т/Р №205 А. Ларина

05 Окт 2017

Категория: 17 (С6) Параметры*Т/P A. Ларина

Задание №18 Т/Р №205 А. Ларина

Елена Репина 2017-10-05 2017-10-04

Смотрите также №13; №14; №15; №16; №17; №19 Тренировочной работы №205 А. Ларина.

18. Найти все значения $a$ , при каждом из которых уравнение

$\sqrt{a-(a+1)(2x+4)}=x+1$

имеет ровно один корень.

Решение:

$\sqrt{a-(a+1)(2x+4)}=x+1;$

$\begin{cases} a-(a+1)(2x+4)=(x+1)^2,& & x+1\geq 0; \end{cases}$

$\begin{cases} x^2+4x+5=-2ax-3a,& & x\geq -1; \end{cases}$

Построим в системе координат $(xoy)$ график функции $y=x^2+4x+5$ при условии $x\geq -1$ – часть параболы $y=(x+2)^2+1,x\geq -1$ с вершиной в точке $(-2;1).$

И будем отслеживать, при каких значениях параметра $a$ прямая $y=-2ax-3a$ будет пересекать указанный кусок параболы ровно один раз.

$y=-2a(x+\frac{3}{2})$ – семейство прямых, проходящих через точку $(-\frac{3}{2};0).$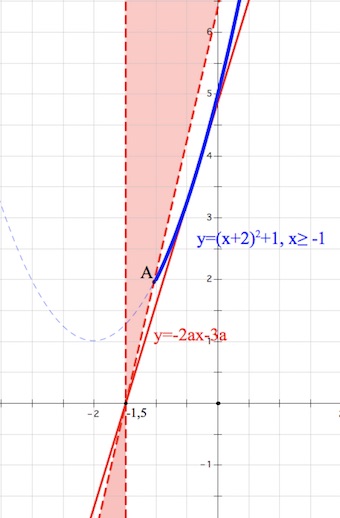

Найдем $a,$ отвечающее за прохождение прямой $y=-2ax-3a$ через точку $A(-1;2)$ (см. рис.)

$2=-2a\cdot (-1)-3a;$

$a=-2.$

Найдем $a,$ отвечающее за касание прямой $y=-2ax-3a$ и части параболы $y=(x+2)^2+1,x\geq -1$ .

Составим в общем виде уравнение касательной к $y=x^2+4x+5$ через точку $(x_0;y(x_0)):$

$y_{kas}=(2x_0+4)(x-x_0)+x_0^2+4x_0+5;$

$y_{kas}=(2x_0+4)x-x_0^2+5.$

Тогда, так как мы полагаем, что и $y=-2ax-3a$ – касательная к $y=x^2+4x+5$ в точке $(x_0;y(x_0)),$ то

$\begin{cases} 2x_0+4=-2a,& &-x_0^2+5=-3a; \end{cases}$

$\begin{cases} -x_0-2=a,& &x_0^2+3x_0+1=0; \end{cases}$

$\begin{cases} a=-\frac{-3\pm \sqrt5}{2}-2,& &x_0=\frac{-3\pm \sqrt5}{2}; \end{cases}$

Так как мы работаем в зоне $x\geq -1,$ то нас интересует точка $x_0=\frac{-3+\sqrt5}{2}.$

Но тогда $a=-\frac{-3+\sqrt5}{2}-2=\frac{-1-\sqrt5}{2}.$

Итак, единственное решение исходное уравнение будет иметь при

$a\in (-\infty;-2)\cup\left \{ \frac{-1-\sqrt5}{2} \right \}.$

При $a\in [-2;\frac{-1-\sqrt5}{2})$ – исходное уравнение будет иметь два решения, при $(\frac{-1-\sqrt5}{2};+\infty)$ – решений нет.

Ответ: $(-\infty;-2)\cup\left \{ \frac{-1-\sqrt5}{2} \right \}.$

Автор: egeMax | Нет комментариев

Печать страницы

Добавить комментарий Отменить ответ

Найти:
Материалы для подготовки к ЕГЭ
№12 №14 №15 №17
Рубрики
- 01 Геометрия (13)
- 02 Стереометрия (9)
- 03 Теория вероятностей ч.1 (1)
- 04 Теория вероятностей ч.2 (1)
- 05 Простейшие уравнения (5)
- 06 Вычисления (5)
- 07 Производная, ПО (4)
- 08 «Прикладные» задачи (5)
- 09 Текстовые задачи (7)
- 10 Графики функций (7)
- 11 Исследование функции (2)
- 12 (С1) Уравнения (78)
- 13 (С2) Стереометр. задачи (94)
- 14 (С3) Неравенства (89)
- 15 (С4) Практич. задачи (71)
- 16 (С5) Планиметр. задачи (86)
- 17 (С6) Параметры* (79)
- 18 (С7) Числа, их свойства (38)
- A1 Простейшие текст/задачи (нет в ЕГЭ-22) (3)
- A2 Читаем графики (нет в ЕГЭ-22) (1)
- Видеоуроки (44)
- ГИА (11)
  - II часть (11)
- ЕГЭ (диагностич. работы) (70)
- Иррациональные выражения, уравнения и неравенства (15)
- Логарифмы (39)
- МГУ (12)
- Метод интервалов (4)
- Метод рационализации (18)
- Модуль (9)
- Параметр (40)
- Переменка (5)
- Планиметрия (60)
- Показательные выражения, уравнения и неравенства (8)
- Разложение на множители (1)
- Рациональные выражения, уравнения и неравенства (10)
- Справочные материалы (92)
- Стереометрия (52)
- Т/P A. Ларина (443)
- Текстовые задачи (12)
- Теория чисел (2)
- Тесты по темам (80)
- Тригонометрические выражения, уравнения и неравенства (43)
- Функции и графики (10)
Дружественные сайты
Сайт А. Ларина ЕгэТренер – О. Себедаш Математика?Легко! Егэ? Ок! – И. Фельдман
Свежие записи
Архивы Архивы