Задание №20 Т/Р №111 А. Ларина

Смотрите также №15, №16, №17, №18, №19.

Найдите все значения $a$, при каждом из которых система уравнений

$\begin{cases}x+\sqrt y=1,\\a+3-\sqrt y=\frac{1}{2}(a-x)^2;&\end{cases}$

имеет единственное решение.

Решение:

$\begin{cases}\sqrt y=1-x,\\a+3+x-1=\frac{1}{2}(a-x)^2;&\end{cases}$

$\begin{cases}\sqrt y=1-x,\\\frac{1}{2}(a-x)^2-x-a-2=0;&\end{cases}$

Необходимо, чтобы уравнение 2-й строки системы имело бы единственный корень при $x\leq 1.$

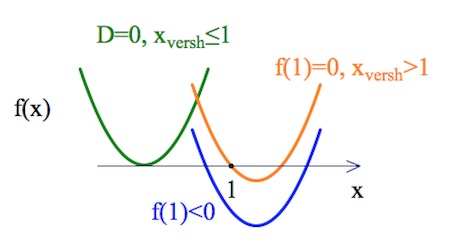
Потребуем (для $f(x)=\frac{1}{2}(a-x)^2-x-a-2$ или, что тоже самое,  для $f(x)=\frac{1}{2}x^2-(a+1)x+\frac{1}{2}a^2-a-2$):

$\left[\begin{array}{rcl}\begin{cases}x_{versh}\leq 1,\\D=0;\end{cases}\\\begin{cases}x_{versh}>1,\\f(1)=0;\end{cases}\end{array}\right.$

$\left[\begin{array}{rcl}\begin{cases}f(1)<0;\end{cases}\\\begin{cases}x_{versh}\leq 1,\\D=0;\end{cases}\\\begin{cases}x_{versh}>1,\\f(1)=0;\end{cases}\end{array}\right.$

$\left[\begin{array}{rcl}\frac{1}{2}-a-1+\frac{1}{2}a^2-a-2<0;\\\begin{cases}a+1\leq 1;\\(a+1)^2-2(\frac{1}{2}a^2-a-2)=0;\end{cases}\\\begin{cases}a+1>1,\\\frac{1}{2}-a-1+\frac{1}{2}a^2-a-2=0;\end{cases}\end{array}\right.$

$\left[\begin{array}{rcl}a^2-4a-5<0;\\\begin{cases}a\leq 0;\\4a+5=0;\end{cases}\\\begin{cases}a>0,\\\left[\begin{array}{rcl}a=-1,\\a=5\end{array}\right.\end{cases}\end{array}\right.$

$\left[\begin{array}{rcl}(a-5)(a+1)<0;\\\begin{cases}a\leq 0;\\a=-\frac{5}{4};\end{cases}\\a=5;\end{array}\right.$

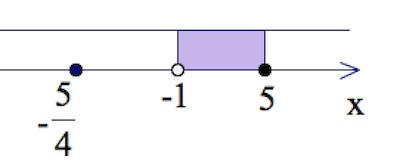
$x\in ${$-\frac{5}{4}$}$\cup (-1;5].$

Ответ: {$-\frac{5}{4}$}$\cup (-1;5].$