Главная › 17 (С6) Параметры* › Задание №20 Т/Р №120 А. Ларина

01 Июн 2015

Категория: 17 (С6) Параметры*ПараметрТ/P A. Ларина

Задание №20 Т/Р №120 А. Ларина

Елена Репина 2015-06-01 2016-07-12

В новом формате ЕГЭ по математике задание значится как «Задание №18»

Смотрите также №15, №16, №17, №18, №19.

Найдите все значения параметра а, при каждом из которых система уравнений

$\begin{cases} \sqrt{y^2+y-20|y|-6x-a+113}+\sqrt{y^2+y+12|y|+10x-a+49}=\sqrt{320},& &x^2-2x-y+a+3=0.& \end{cases}$

имее ровно два решения.

Решение:

$\begin{cases} \sqrt{(y^2-20|y|+100)+(y-a)-6x+13}+\sqrt{(y^2+12|y|+36)+(y-a)+10x+13}=\sqrt{320},& &y-a=x^2-2x+3.& \end{cases}$

$\begin{cases} \sqrt{(|y|-10)^2+(x-4)^2}+\sqrt{(|y|+6)^2+(x+4)^2}=\sqrt{320},& &y-a=x^2-2x+3.& \end{cases}$

$\begin{cases} \sqrt{(x-4)^2+(|y|-10)^2}+\sqrt{(x+4)^2+(|y|+6)^2}=\sqrt{320},& &y=(x-1)^2+2+a.& \end{cases}$

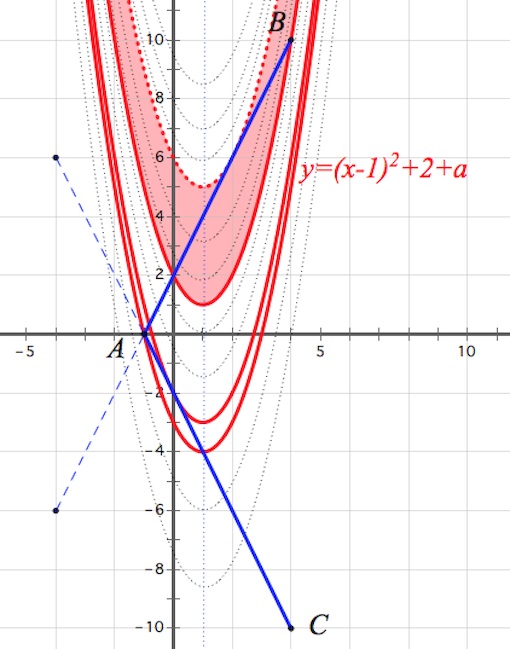
Первая строка системы задает объединение отрезков с концами $A(-4;-6),B(4;10)$ ; $A(-4;6),C(4;-10).$

Действительно, при $y\geq 0$ первая строка системы приобретает вид:

$\sqrt{(x-4)^2+(y-10)^2}+\sqrt{(x+4)^2+(y+6)^2}=\sqrt{320}$

Левая часть уравнения – есть сумма расстояний от некоторой точки $(x;y)$ до точек $(4;10)$ и $(-4;-6)$ , при этом расстояние между точками $(4;10)$ и $(-4;-6)$ равно $\sqrt{(4+4)^2+(10+6)^2}=\sqrt{320}$ . Вспоминаем, что $y\geq 0$ , поэтому произвольная точка $(x;y)$ ( $y\geq 0$ ) – точка отрезка с концами $A(-4;-6)$ и $B(4;10)$ .

Аналогичные рассуждения будут и при $y<0.$

Вторая строка системы задает семейство парабол c центром на прямой $x=1.$

0ij

Случай 1.

Во-первых, найдем $a$ , отвечающее за касание параболы $y=(x-1)^2+2+a$ и отрезка $AB$ (уравнение отрезка $AB$ можно записать так: $y=2x+2,$ $-1\leq x\leq 4$ ).

Потребуем, чтобы $D=0$ для $(x-1)^2+2+a=2x+2$ при $-1\leq x\leq 4$ .

Так как для $x^2-4x+1+a=0$ $D/4=3-a$ , то $a=3.$

Во-вторых, найдем $a$ , отвечающее за прохождение параболы $y=(x-1)^2+2+a$ через точку $B(4;10).$

$10=(4-1)^2+2+a;$

$a=-1.$

Итак, при $a\in [-1;3)$ имеем две точки пересечения параболы $y=(x-1)^2+2+a$ и ломаной $BAC$ . То есть при $a\in [-1;3)$ исходная система имеет два решения, что нас устраивает.

Случай 2.

Найдем $a$ , отвечающее за прохождение параболы $y=(x-1)^2+2+a$ через точку $A(-1;0)$ .

Поэтому подходящее нам $a$ ищем из уравнения:

$0=(-1-1)^2+2+a;$

$a=-6.$

При найденном значении $a$ система имеет два решения.

Случай 3.

Найдем $a$ , отвечающее за касание параболы $y=(x-1)^2+2+a$ и отрезка $AC$ (уравнение отрезка $AC$ можно записать так: $y=-2x-2,$ $-1\leq x\leq 4$ ).

Потребуем, чтобы $D=0$ для $(x-1)^2+2+a=-2x-2$ при $-1\leq x\leq 4$ .

Так как для $x^2+5+a=0$ $D=-5-a$ , то $a=-5.$

При найденном значении $a$ парабола имеет две точки с ломаной $BAC$ .

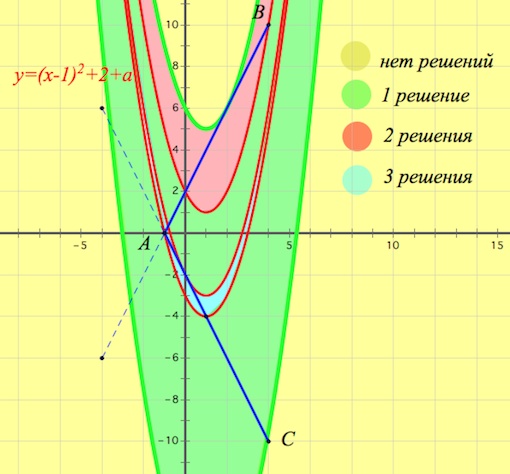
Ответ: { $-6;-5$ } $\cup [-1;3)$ .

Автор: egeMax | комментария 24

Печать страницы

комментария 24

Дима

2015-06-01 в 12:49

Или Вы сделали ту же ошибку, что и я, или мы сделали правильно.
Разве не должен быть угол, а не крестик? То есть Вы рисуете оба отрезка, не ограничивая на положительность/отрицательность координаты У.

[ Ответить ]
- egeMax
  
  2015-06-01 в 13:52
  
  Дим, спасибо большое! Спешка… :(
  Исправлено.
  
  [ Ответить ]
  - Дима
    
    2015-06-01 в 17:09
    
    Да не за что, и сам так ошибся. Самое интересное то, что это не влияет на ответ вообще:)
    А 120+ будет? Очень интересна заадча с мячиками…
    
    [ Ответить ]
    - egeMax
      
      2015-06-01 в 17:50
      
      Дима, насчет 120+ не знаю… Не успеваю… Аврал с учениками…
      
      [ Ответить ]
      - Дима
        
        2015-06-01 в 20:58
        
        Да оно как бы и не очень надо, можете потом 16-ую выложить? Интересно просто)
        
        [ Ответить ]
      - egeMax
        
        2015-06-01 в 21:19
        
        Быть может… но не раньше среды…
        
        [ Ответить ]
    - egeMax
      
      2015-06-02 в 21:55
      
      Дима, №16 Т/Р №120+ готов.
      
      [ Ответить ]
      - .
        
        2015-07-29 в 11:30
        
        Посоветуйте пожалуйста пособия для подготовки к заданиям с параметров, которые вы использовали
        
        [ Ответить ]
      - egeMax
        
        2015-07-29 в 11:37
        
        Можете обратиться, например, к
        
        Прокофьев А.А. Задачи с параметрами. Москва МИЭТ 2004. или вот
        
        [ Ответить ]
Алексей

2015-06-01 в 18:30

{-6;-5} то есть а=-6 и а=-5?
а=-6 получилась. Не могу понять откуда а=-5
и что это за уравнение в 3 случае “Так как для x^2+5+a=0”?

[ Ответить ]
- egeMax
  
  2015-06-01 в 20:50
  
  а=-5 как раз и выскакивает в третьем случае. Следует потребовать, чтобы дискриминант для x^2+5+a=0 равнялся бы нулю. Откуда a=-5.
  
  [ Ответить ]
Михаил

2015-06-02 в 13:38

не могу понять ваши преобразования вначале. подскажите пожалуйста

[ Ответить ]
- egeMax
  
  2015-06-02 в 15:12
  
  Из второй строки системы выразили y-a и подставили в первую. Затем выделяем полные квадраты.
  Все равно не ясно?
  
  [ Ответить ]
Софья

2015-06-02 в 15:43

При виде таких заданий хочется забиться в угол, и плакать, плакать, плакать.

[ Ответить ]
- egeMax
  
  2015-06-02 в 15:45
  
  Софья, не самое подходящее время для этого. До экзамена – считанные часы. Не теряйте время и не отчаивайтесь! Удачи!
  
  [ Ответить ]
Елена

2015-06-05 в 09:45

Елена, спасибо огромное за тренинг.На ЕГЭ вчера были окружности.

[ Ответить ]
- egeMax
  
  2015-06-05 в 13:19
  
  Елена, за тренинг?
  
  [ Ответить ]
- Pasha
  
  2015-09-15 в 20:46
  
  Скажите, пожалуйста, по каким сборникам вы готовились к егэ?
  
  [ Ответить ]
  - egeMax
    
    2015-09-15 в 20:55
    
    Полагаю вопрос таков: “по каким сборникам готовиться к егэ”?
    Например, C1, С2, … Загляните на сайт А. Ларина. В правой колонке обратите внимание на цветные квадратики )))
    
    [ Ответить ]
Максим

2015-10-28 в 15:16

Первая строка системы задает объединение отрезков с концами A(-1;0),B(4;10); A(-1;0),C(4;-10). Почему A(-1;0)?

[ Ответить ]
- egeMax
  
  2015-10-28 в 22:16
  
  Максим, исправлено. Спасибо.
  
  [ Ответить ]
  - Максим
    
    2015-11-06 в 16:29
    
    нет, там вроде правильно было, просто я не понимаю откуда оно взялось?
    
    [ Ответить ]
    - egeMax
      
      2015-11-06 в 20:45
      
      Вам следует вспомнить, как вычисляется расстояние между точками.
      Если $A(a_1;a_2),B (b_1;b_2)$ , то $AB=\sqrt{(a_1-b_1)^2+(a_2-b_2)^2}$ .
      Так $\sqrt{(x-1)^2+(y-2)^2}$ , например, есть расстояние между точками $(1;2)$ и $(x;y)$ .
      А уже $\sqrt{(x-1)^2+(y-2)^2}+\sqrt{(x-3)^2+(y+2)^2}$ , например, уже есть сумма расстояний… (продолжите сами).
      Так вот точка $(x;y)$ может гулять по отрезку с концами $(1;2)$ и $(3;-2)$ , а может быть вне его. Если указанная сумма будет равняться $2$ (а именно длина отрезка с концами $(1;2)$ и $(3;-2)$ и есть $2$ ), то точка $(x;y)$ гуляет по отрезку с концами $(1;2)$ и $(3;-2)$ . То есть $\sqrt{(x-1)^2+(y-2)^2}+\sqrt{(x-3)^2+(y+2)^2}=4$ задает отрезок с концами $(1;2)$ и $(3;-2)$ .
      Понятно ли так?
      
      [ Ответить ]
    - Лена
      
      2016-05-05 в 12:55
      
      A(-4;-6),B(4;10) при у=<0, значит все что ниже у=0 откидывается
      
      [ Ответить ]

Задание №20 Т/Р №120 А. Ларина

Добавить комментарий Отменить ответ