Задача 1. Высота конуса равна $12$, образующая равна $14.$ Найдите его объем, деленный на $\pi$.
Решение: + показать
Объем конуса вычисляется по формуле $V=\frac{\pi R^2H}{3},$ где $R$ – радиус основания, $H$ – высота конуса.
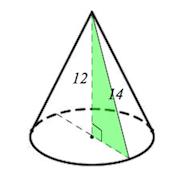
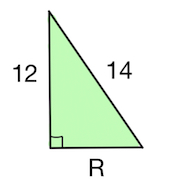 Находим радиус основания $R$ по т. Пифагора (см. на рисунке зеленый прямоугольный треугольник):
Находим радиус основания $R$ по т. Пифагора (см. на рисунке зеленый прямоугольный треугольник):
$R^2=14^2-12^2=(14-12)(14+12)=52.$
Тогда
$V=\frac{\pi \cdot 52\cdot 12}{3}=208\pi.$
Откуда
$\frac{V}{\pi}=208.$
Ответ: $208.$
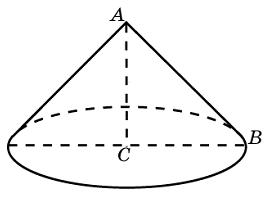
Задача 2. Конус получается при вращении равнобедренного прямоугольного треугольника $ABC$ вокруг катета, равного $6.$ Найдите его объем, деленный на $\pi$.
Решение: + показать
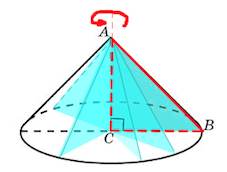
В качестве высоты конуса выступает катет треугольника, равный $6.$ В качестве радиуса основания конуса – второй катет треугольника, равны также $6.$
Поэтому
$V=\frac{\pi R^2H}{3}=\frac{\pi\cdot 6^2\cdot 6}{3}=72\pi.$
Тогда
$\frac{V}{\pi}=72.$
Ответ: $72.$
Задача 3. Высота конуса равна $15,$ а диаметр основания – $16.$ Найдите образующую конуса.
 Решение: + показать
Решение: + показать
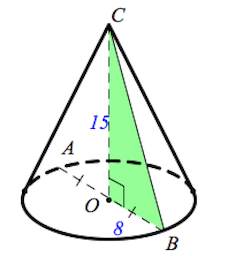
Найдем образующую конуса $BC$ из прямоугольного треугольника $BCO$ по т. Пифагора.
При этом заметим, что
$BO=R=\frac{AB}{2}=8;$
$BC=\sqrt{OC^2+OB^2};$
$BC=\sqrt{15^2+8^2}=17.$
Ответ: $17.$
Задача 4. Найдите объем $V$ конуса, образующая которого равна $3$ и наклонена к плоскости основания под углом $30°.$ В ответе укажите $\frac{V}{\pi}.$
Решение: + показать
$V=\frac{\pi R^2\cdot H}{3},$
где $R$ – радиус основания конуса, $H$ – высота
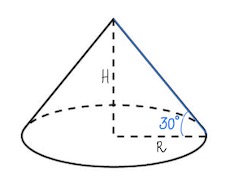
Высота конуса как катет напротив угла в $30^{\circ}$ равен половине гипотенузы длиной $3$, то есть равен $\frac{3}{2}.$
При этом по теореме Пифагора
$R^2=3^2-(\frac{3}{2})^2=\frac{27}{4}.$
Тогда
$V=\frac{\pi\cdot \frac{27}{4}\cdot \frac{3}{2}}{3}=\frac{27}{8}=3,375$
Ответ: $3,375.$
Задача 5. Длина окружности основания конуса равна $5,$ образующая равна $8.$ Найдите площадь боковой поверхности конуса.

Решение: + показать
Площадь боковой поверхности конуса есть
$S_{bok}=\pi RL$,
где $R,\;L$ – радиус основания конуса и образующая конуса.
А поскольку длина окружности основания конуса равна $2\pi R$ и равна $5$ по условию, то
$5=2\pi R;$
$\pi R=2,5.$
Тогда
$S_{bok}=\pi RL=2,5\cdot 8=20.$
Ответ: $20.$
Задача 6. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в $9$ раз?

Решение: + показать
Площадь боковой поверхности конуса зависит от двух величин – от $R$ и $L$, так как
$S_{bok}=\pi RL$
($R,\;L$ – радиус, образующая конуса)
Радиус не изменяется, а образующая увеличивается в $9$ раз. Значит и площадь боковой поверхности конуса увеличится в $9$ раз.
Ответ: $9.$
Задача 7. Во сколько раз уменьшится объем конуса, если его высоту уменьшить в $6$ раз?

Решение: + показать
$V=\frac{\pi R^2H}{3}$ – объем конуса.
Если высоту уменьшаем в $6$ раз, то и объем уменьшается в $6$ раз.
Ответ: $6.$
Задача 8. Во сколько раз увеличится объем конуса, если радиус его основания увеличится в $17$ раз, а высота останется прежней?

Решение: + показать
$V=\frac{\pi R^2H}{3}$ – объем конуса.
Увеличение радиуса основания в $17$ раз повлечет за собой увеличение объема конуса в $17^2,$ то есть в $289$ раз.
Ответ: $289.$
Задача 9. Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.
Решение: + показать
Согласно условию
$2\pi R^2=\pi RL$
($R,\;L$ – радиус основания конуса, образующая конуса).
Откуда
$R=\frac{L}{2}.$
Прямоугольный треугольник, образованный высотой, образующей и радиусом основания таков, что катет, равный радиусу, вдвое меньше гипотенузы, значит угол между образующей конуса и плоскостью основания равен $60^{\circ}.$
Ответ: $60.$
Задача 10. Объем конуса равен $10.$ Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
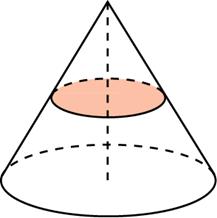
Решение: + показать
Отсекаемый конус подобен исходному и $k=2$ – коэффициент подобия.
Как известно, объемы подобных тел находятся в отношении $k^3,$ где $k$ – коэффициент подобия. Тогда объем отсекаемого конуса в $8$ раз (так как $k^3=8$) меньше объема исходного, то есть равен $\frac{10}{8}=1,25.$
Ответ: $1,25.$
Задача 11. Площадь полной поверхности конуса равна $148.$ Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.

Решение: + показать
Малый отсеченный конус подобен исходному с коэффициентом подобия $2.$ Площади поверхностей подобных тел находятся в отношении $k^2,$ где $k$ – коэффициент подобия. Поэтому площади поверхностей будут отличаться в $4$ раза.
Значит, площадь полной поверхности отсеченного конуса есть $\frac{148}{4}=37.$
Ответ: $37.$
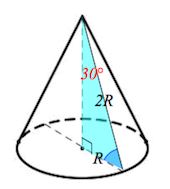
Задача 12. Найдите объем $V$ конуса, образующая которого равна $11$ и наклонена к плоскости основания под углом $30^{\circ}.$ В ответе укажите $\frac{V}{\pi}$.
Решение: + показать
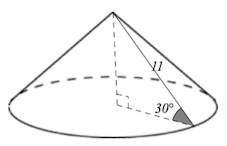
$V=\frac{\pi R^2H}{3}$,
где $H=\frac{11}{2}$ (так как напротив угла 30° лежит катет, вдвое меньший гипотенузы ($L$))
и
$R^2=11^2-(\frac{11}{2})^2=\frac{3\cdot 11^2}{4}$.
Поэтому
$V=\frac{\pi \cdot \frac{3\cdot 11^2}{4}\cdot \frac{11}{2}}{3}=166,375\pi.$
Откуда
$\frac{V}{\pi}=166,375.$
Ответ: $166,375.$
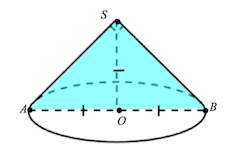
Задача 13. Диаметр основания конуса равен $66,$ а угол при вершине осевого сечения равен $90$°. Вычислите объем конуса, деленный на $\pi$.
Решение: + показать
 Для того, чтобы найти объем, нам нужно найти радиус основания $R$ и высоту конуса $H,$ так как
Для того, чтобы найти объем, нам нужно найти радиус основания $R$ и высоту конуса $H,$ так как
$V=\frac{\pi R^2H}{3}$
Треугольник $ASB$, образованный диаметром и соответствующими образующими, – прямоугольный и равнобедренный.
Середина $O$ гипотенузы $AB$ является центром описанной окружности около треугольника $ASB$. А значит $SO=AO=BO$. Поэтому, так как диаметр основания равен $66,$ то $R=H=33.$
Наконец,
$V=\frac{\pi 33^2\cdot 33}{3}=11979\pi.$
Откуда
$\frac{V}{\pi}=11979.$
Ответ: $11979.$
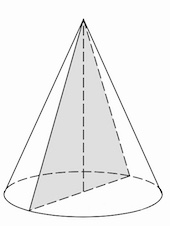
Задача 14. Площадь основания конуса равна $36\pi$, высота — $3.$ Найдите площадь осевого сечения конуса.
Решение: + показать
Согласно условию
$\pi r^2=36\pi;$
$r=6.$
Осевое сечение конуса – равнобедренный треугольник с основанием $2r=12$ и высотой $3$, проведенной к этому основанию.
Значит,
$S_{sech}=\frac{12\cdot 3}{2}=18.$
Ответ: $18.$
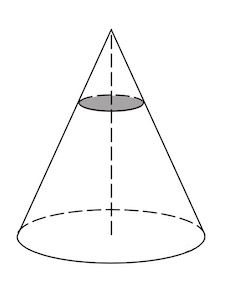
Задача 15. Площадь основания конуса равна $48.$ Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной $15$ и $45,$ считая от вершины. Найдите площадь сечения конуса этой плоскостью.
Решение: + показать
Плоскость, параллельная основанию, отсекает конус, подобный исходному и коэффициент подобия $k=\frac{60}{15}=4.$ Площади оснований конусов отличаются тогда в $k^2=16$ раз.
Тогда площадь сечения конуса указанной плоскостью равна $\frac{48}{16}=3.$
Ответ: $3.$
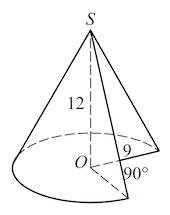
Задача 16. Найдите объем $V$ части конуса, изображенной на рисунке. В ответе укажите $\frac{V}{\pi}$.
Решение: + показать
Часть конуса, изображенная на рисунке – это $\frac{3}{4}$ часть конуса с радиусом основания $9$ и высотой $12.$
Поэтому
$V=\frac{3}{4}\cdot \frac{\pi R^2H}{3}=\frac{3\pi \cdot 9^2\cdot 12}{12}=243\pi.$
Откуда
$\frac{V}{\pi}=243.$
Ответ: $243.$
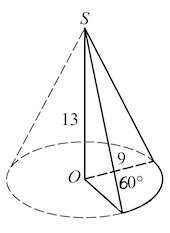
Задача 17. Найдите объем $V$ части конуса, изображенной на рисунке. В ответе укажите $\frac{V}{\pi}$.
Решение: + показать
Часть конуса, изображенная на рисунке – это $\frac{1}{6}$ часть конуса с радиусом основания $9$ и высотой $13.$
Поэтому $V=\frac{1}{6}\cdot \frac{\pi R^2H}{3}=\frac{\pi \cdot 5 \cdot 9^2\cdot 13}{18}=292,5\pi.$
Откуда $\frac{V}{\pi}=292,5.$
Ответ: $292,5.$
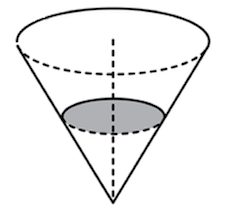
Задача 18. В сосуде, имеющем форму конуса, уровень жидкости достигает $\frac{1}{2}$ высоты. Объём жидкости равен $54$ мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
Решение: + показать
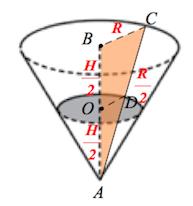
Отсеченный конус, образовавшийся при пересечении исходного конуса плоскостью параллельной основанию и пересекающей высоту конуса посередине, подобен исходному с коэффициентом подобия $k=2.$
Так как объемы подобных тел находятся в отношении $k^3$, где $k$ – коэффициент подобия, то объем исходного конуса есть $8$ объемов отсеченного конуса ). Стало быть, на усеченный конус приходится $7$ объемов отсеченного (малого) конуса.
То есть объем усеченного конуса (а значит объем жидкости, что нужно долить) есть $7\cdot 54=378.$
Ответ: $378.$

Вы можете пройти тест


 Решение: + показать
Решение: + показать

























 Для того, чтобы найти объем, нам нужно найти радиус основания $R$ и высоту конуса $H,$ так как
Для того, чтобы найти объем, нам нужно найти радиус основания $R$ и высоту конуса $H,$ так как
Скажите пожалуйста,почему в 17 задаче вы сосуд рассматриваете как перевёрнутый конус вверх дном,а не наоборот.Если рассуждать логически то сосуд не устоит на высоте конуса и ответ в этой задачи получится совершенно другой
Андрей, расскажите какой ответ у вас получается? Очень интересно…
6,75
К данной задаче как раз-таки прилагается картинка с вершиной вниз.
Андрей, мы не должны заботится в задаче о том, как удерживается сосуд (может его зажим какой держит, – нам-то какое дело…). Мне как раз-таки непонятно, как вы собираетесь наполнять сосуд в виде конуса, если поставите его на основание…
В 5-ой задаче вместо 2пиR^2=пиRL должно быть пиR^2=2пиRL
Михаил, вы ошибаетесь!
Объясните пожалуйста почему в пятой задачке 2пиR^2=пиRL а не 2пиRL=пиR^2, ведь по условию площадь боковой поверхности (пиRL) в два раза больше площади основания (пиR^2)
Наруто, вы сами себе противоречите…
Если вы умножите, и без того бОльшую, площадь боковой поверхности, на 2, то как новое выражение сравняется с меньшим?
подскажите пожалуйста как расчитать угол наклона конуса если известны D=90 и l=60
Рассмотрите прямоугольный треугольник с катетами радиус+высота, гипотенуза – образующая. Косинус угла есть 45:60, то есть 3:4